【力学】加速度①（加速度の概要）

2021年5月19日

加速度

直線運動の加速度

車を運転する場合を考えましょう。時速50キロの道を走るとします。信号待ちが終わり、出発します。このとき、突然50キロの速度で進むわけではないですよね。停止している状態（つまり0キロ）から少しずつ速くなっていき最終的に50キロでアクセルを強めるのをストップするわけです。

この少しずつ速くなっていく状態を加速しているって言いますよね。この加速度合いを表しているのが加速度です。速度が時間とともに変化する運動を加速度運動と言います。

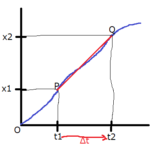
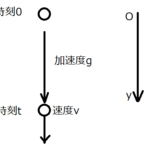
加速度を求める公式について考えていきます。一直線上を運動している物体で、時刻\(t_1[s]\)での物体の速度を\(v_1[m/s]\)、\(t_2[s]\)（\(t_1<t_2\)）での速度を\(v_2[m/s]\)とします。経過時間\(\Delta t=t_2-t_1\)の間に速度が\(\Delta v=v_2-v_1\)だけ変化しています。この間の1秒当たりの速度の変化、つまり平均の加速度\(\bar{a}\)は、

\[\bar{a}=\frac{\text{速度の変化}}{\text{経過時間}}=\frac{v_2-v_1}{t_2-t_1}=\frac{\Delta v}{\Delta t}\text{・・・(11)}\]

加速度の単位は、\(m/s^2\)と表して【メートル毎秒毎秒】と読みます。\(1m/s^2\)は、1秒間に速度が1m/sの割合で変化する場合の加速度です。

加速度の向き

加速度も、速度と同じように、大きさだけでなく向きについての情報も持ち合わせています。つまり、ベクトルです。

速度が上昇している状態・つまり加速している状態のときは加速度は正となり、速度が減少している状態・つまり減速している状態のときは加速度は負となります。

たとえば、40キロで走っていた車が2秒後に20キロに減速していた場合、速度は正ですが、加速度は負になります。

瞬間の加速度

平均の速度から瞬間の速度を考えるとき、瞬間の速度は\(x-t\)グラフ上の接線の傾きで表されるというのがありました。瞬間の速度についてはコチラ↓

これと同じ考え方を加速度にも取り入れます。つまり、瞬間の加速度は、\(v-t\)グラフ上の接線の傾きで表されます。\(v-t\)グラフとは、縦軸を速度\(v\)、横軸を時間\(t\)で表しているグラフのことです。

平面運動の加速度

\(t_1[s]\)のときに北向きに\(v_1[m/s]\)だった車が、\(t_2[s]\)のときに東向きに\(v_2[m/s]\)になった時を考えます。

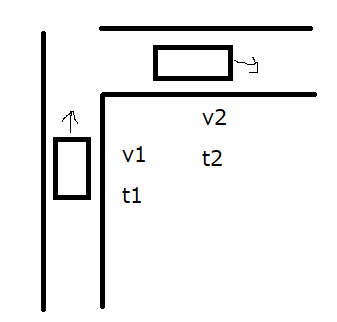
このときの加速度\(\vec{a}\)は、以下のように求めることができます。

\[\vec{a}=\frac{\vec{v2}-\vec{v_1}}{t_2-t_1}\text{・・・}(12)\]

まとめ

今回の重要事項としては…

今回の内容は以上です。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。