【2次関数】センター試験の問題を解いてみる（2004年度）

2021年5月15日

2004年度の問題はコチラ↓

問題【前編】

解答（解説）【前編】

グラフの頂点は平方完成によって求めます。平方完成については過去に解説していますので↓からどうぞ。

グラフの式は\(y=-x^2+(2a-5)x-2a^2+5a+3\)です。これを平方完成すると、

\(y=- \left(x-\frac{2a-5}{2} \right)^2+\frac{-4a^2+37}{4}\)

したがって、関数\(C\)の頂点は、

\[\left(\frac{2a-5}{2},\frac{-4a^2+37}{4}\right)\]

問題【後編】

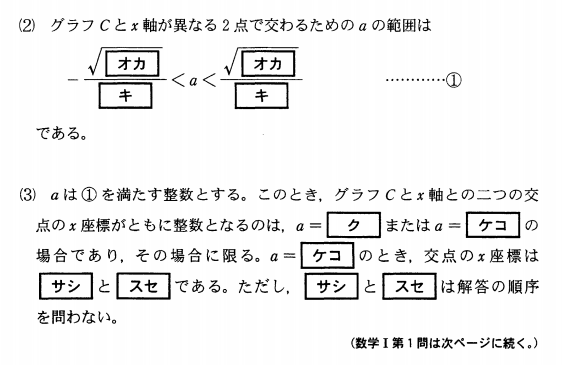
解答（解説）【後編】

オ・カ・キ

グラフと\(x\)軸が異なる2点で交わる条件は判別式\(D>0\)です。

\(D=b^2-4ac=(2a-5)^2-4\cdot(-1)\cdot(-2a^2+5a+3)\)より、

\((2a-5)^2-4\cdot(-1)\cdot(-2a^2+5a+3)>0\)

したがって、

\[-\frac{\sqrt{37}}{2}<a<\frac{\sqrt{37}}{2}\]

ク・ケ・コ

\(a\)は\(-\frac{\sqrt{37}}{2}<a<\frac{\sqrt{37}}{2}\)を満たす整数だそうです。

\(\sqrt{37}\)は、6から7の間の大きさです。6が\(\sqrt{36}\)と等しいですからね。したがって、\(\frac{\sqrt{37}}{2}\)は、3より大きく4より小さい数になりそうです。

以上を踏まえると、\(-\frac{\sqrt{37}}{2}<a<\frac{\sqrt{37}}{2}\)を満たす整数は、-3から3までですね。

\(x\)軸との交点の\(x\)座標を求めるためには、関数式に\(y=0\)を代入すればよいです。

\(-x^2+(2a-5)x-2a^2+5a+3=0\)

これを解くと、\(x=\frac{2a-5\pm\sqrt{-4a^2+37}}{2}\)

ここで、赤線部分で求めた\(a=-3,-2,-1,0,1,2,3\)を1つずつ\(\sqrt{-4a^2+37}\)に代入していきましょう。ルートが外れない\(a\)の値は除外していきましょう。すると、残るのは\(a=3,-3\)の2つです。

したがって、今回求める\(a\)の値は

\[a=3,-3\]

サ・シ　ス・セ

\(x=\frac{2a-5\pm\sqrt{-4a^2+37}}{2}\)に\(a=-3\)を代入しましょう。

すると、\(x=-6,-5\)

したがって、解答は

\[x=-6,-5\]

まとめ

今回の問題を解く上での重要なポイントをまとめてみました。

というわけで、今回の内容は以上です。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。