【力学】速度④(相対速度)
速度①②③はこちら↓
相対速度
直線上の相対速度
高速道路を2台のバスが走っています。それぞれ、\(80km/h\)、\(100km/h\)で走っているとしましょう。\(80km/h\)の方をA、\(100km/h\)の方をBとします。バスの進行方向を正の向きとします。
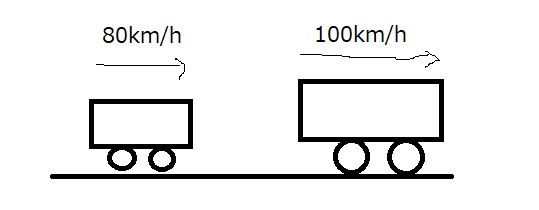
静止している人から見れば、Aは\(80km/h\)であり、Bは\(100km/h\)に見えます。当たり前ですね。
では視点を変えてみましょう。AからBを見た時、どのように見えるでしょうか。\(20km/h\)の速さで正の方向に遠ざかっていくように見えるかと思います。つまり、Aから見たBの速度は\(20km/h\)です。
一方、BからAを見た時、どのように見えるでしょうか。\(20km/h\)の速さで負の方向に遠ざかっていくように見えますね。したがって、Bから見たAの速度は\(-20km/h\)です。
このように、自分から見た相手の速度のことを、自分に対する相手の相対速度といいます。相対速度は、相手の速度から自分の速度を引くことによって得られます。
\[v=v_{\text{相手}}-v_{\text{自分}} \text{・・・(9)}\]
\(v_{\text{相手}}\) : 相手の速度
\(v_{\text{自分}}\) : 自分の速度
ベクトル
平面上の相対速度の説明をする前に、ベクトルについて少し解説をします。平面上の相対速度について理解するために必要なベクトルの知識として、ベクトルの和と差があります。実際にはベクトルの差が理解できていればいいのですが、ベクトルの差を理解するためにベクトルの和の説明が不可欠なので一緒に説明します。
ベクトルの和
ベクトルの和と差は平行四辺形の法則によって得られます。たとえば、下図のような\(\vec{a}\)と\(\vec{b}\)があったとします。

このとき、平行四辺形の法則により、\(\vec{a}+\vec{b}\)は以下のようになります。
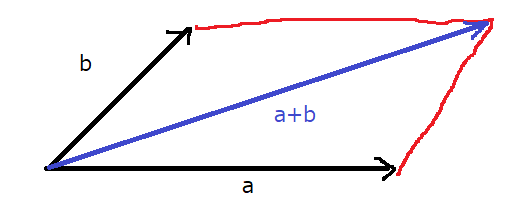
ベクトルの差
\(\vec{b}-\vec{a}\)は、次のようになります。
\(\vec{b}-\vec{a}=\vec{b}+(-\vec{a})\)なので…
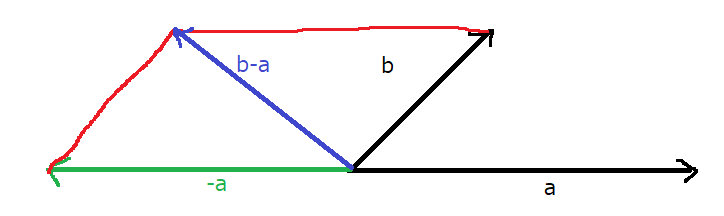
\(\vec{a}\)を逆方向に引っ張って\(\vec{b}\)との和をとることにより、得ることができます。
ここまでの内容を踏まえて、平面上の相対速度について解説していきます。
平面上の相対速度
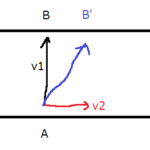
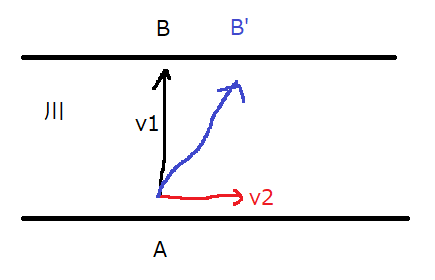
AとBの2台のバスが、次のように異なる方向に進む場合を考えます。

Aの速度を\(\vec{a}\)とします。Bの速度を\(\vec{b}\)とします。このとき、Aに乗っている人がBを見た時、つまりAに対するBの相対速度を求めてみましょう。
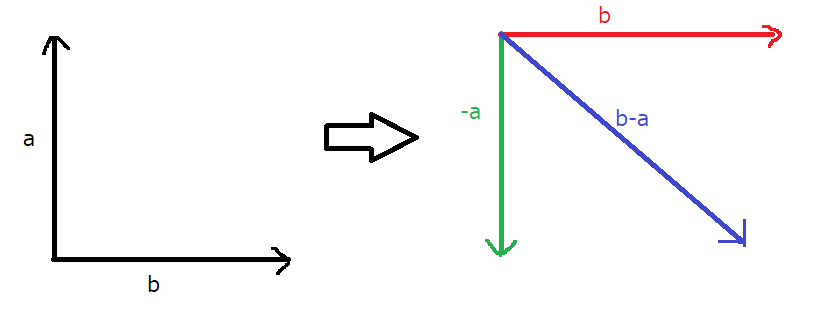
\(\vec{a}\)の向きを逆に変えることで\(-\vec{a}\)が得られます。\(\vec{b}\)を平行移動することにより、青線で示すような\(\vec{b}-\vec{a}\)を得ることができます。つまり、AからBを見ると、青線の方向、つまり右下方向に離れていくように見えるわけですね。
したがって、Aに対するBの相対速度\(\vec{v_{AB}}\)は次のように求められます。
\[\vec{v_{AB}}=\vec{v_B}-\vec{v_A}\text{・・・(10)}\]
雨が鉛直に降る中を、電車がまっすぐな線路上を一定の速さ\(10\sqrt{3}m/s\)で水平に走っている。雨粒の落下の速さを\(10m/s\)とする。
(1)電車内の人が窓から見る雨粒の落下方向と鉛直方向がなす角の大きさを求めよ。
(2)電車内の人が窓から見る雨粒の速さを求めよ。
(1)電車の速度を\(\vec{v_A}\)、雨の速度を\(\vec{v_B}\)、電車内の人から見た雨粒の相対速度を\(\vec{v_{AB}}\)とします。
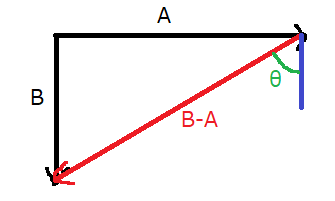
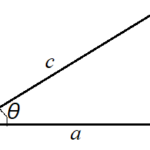
\(\tan\theta=\frac{10\sqrt{3}}{10}=\sqrt{3}\)より、\(\theta=60^\circ\)
(2)\(\vec{v_{AB}}\)の大きさを\(AB\)とすると、
\(AB\cos 60^\circ=10\)より、\(AB\times\frac{1}{2}=10\)
\(AB=20\)
したがって、\(\vec{v_{AB}}\)の大きさ=\(20m/s\)
まとめ
- 自分から見た相手の速度を、自分に対する相手の相対速度という。
- 相対速度は、以下のようにして求められる。
- 直線上:\(v_{AB}=v_B-v_A\)
- 平面上:\(\vec{v_{AB}}=\vec{v_B}-\vec{v_A}\)
ベクトルと三角関数の合わせ技です(笑)。数学が苦手な方はこの辺で既に拒否反応ですよね…。私が学生時代に物理の授業を受けているとき、友人の中にはこの辺からしんどくなった人もいたようで、テスト前とかよく教えを請われたのを覚えています…(笑)
物理の勉強の前に三角比・三角関数・ベクトルについては一通り勉強しておいた方がいいと思います。
というわけで、今回の内容はここまでです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。