【力学】速度②(平均の速度・瞬間の速度など)
速度①についてはコチラ↓
等速直線運動などを説明しています。
速度
「速さ」と「速度」は違います。「速さ」は速度の大きさのみを表すものであり、向きは関係ありません。一方、「速度」は大きさと"向き“の2つの情報で表します。
例えば、ある一つの道路に2つの車が走っていたとしましょう。A車は東向きに10m/sで、B車は西向きに10m/sで走っているとします。このとき、A車とB車の速さは、どちらも10m/sで等しいです。しかし、向きは逆ですよね。速度を表すときには、向きも考えなければならないんですね。
「速度」のように、大きさと向きをもつ量を一般的にベクトルといいます。記号では、\(\vec{v}\)のように、文字の上に矢印を付けて表します。ベクトルについての詳細は数学の内容になるので、今回は割愛します。
一直線上の運動では、ある一方の方向を正の向きと定めることで、速度の向きを正・負の符号によって表すことができます。先程の例で、東向きに10m/s、西向きに10m/sとしましたが、東向きの方向を正とすると、A車の速度は\(v\)=10m/s、B車の速度は\(v\)=-10m/sです。
ちなみに、速さは向きは関係なく「大きさ」のみで表せます。このように、大きさだけで定まる量をスカラーといいます。大きさと向きをもつ速度などはベクトルといいます。
変位
物体の位置の変化を変位といいます。位置の変化というのは、どれだけ移動したかということです。速度と同様に、変位も大きさと向きをもつベクトルです。
一直線上の運動で、運動の向きが変わらない場合は、移動距離と変位は等しいです。しかし、途中で折り返したり曲がる場合には変位の大きさと移動距離は異なります。
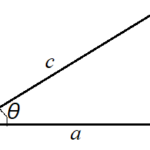
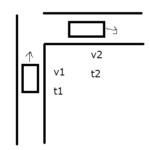
例えば、50メートル走の場合は移動距離と変位はともに50メートルです。しかし、100メートル走で50メートル先のポールを折り返してスタート地点まで戻ってくる場合、移動距離は100メートルですが、変位は0メートルです。また、下図のように50メートル走った先の交差点を右折して50メートル走った場合は、移動距離は100メートルですが、変位は約70メートルになります。
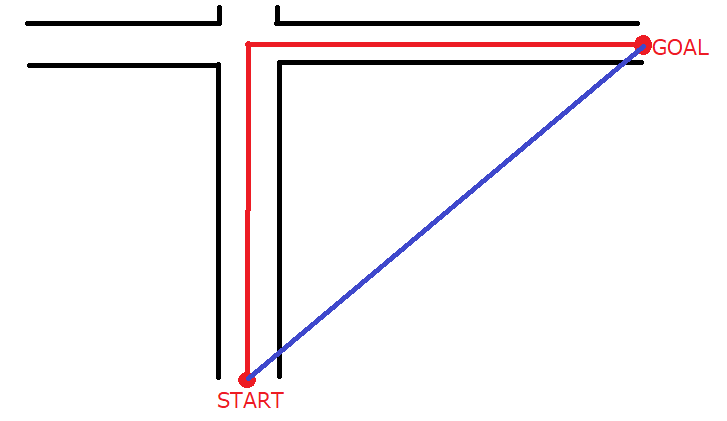
変位の計算↓
\(\text{変位}=\sqrt{50^2+50^2}=\sqrt{5000}=50\sqrt{2}\text{≒}50\times1.4=70\)
平均の速度
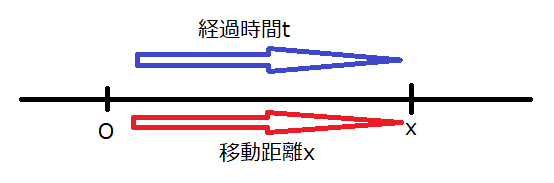
下図のような一直線上を物体が動く状況を考えます。
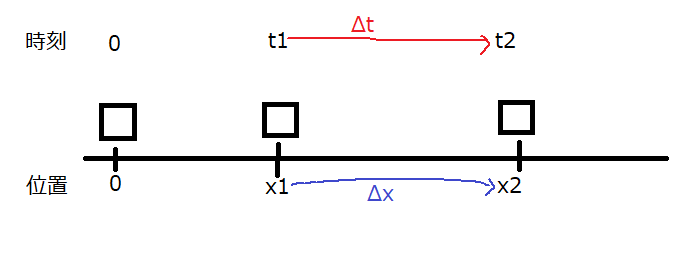
時刻\(t_1\)[s]での物体の位置を\(x_1\)[m]、時刻\(t_2\)[s]での位置を\(x_2\)[m]とします。この2点の間の変位\(\Delta x\)は\(x_2-x_1\)、経過時間\(\Delta t\)は\(t_2-t_1\)で表せます。このとき、
\[\bar{v}=\frac{x_2-x_1}{t_2-t_1}=\frac{\Delta x}{\Delta t}\text{・・・③}\]
は、この区間における単位時間当たりの変位を表します。こうして求められる速度\(\bar{v}\)を平均の速度といいます。
瞬間の速度
③式について、\(t_2\)を\(t_1\)に限りなく近づけていきます。つまり、\(\Delta t\)を小さくしていくわけですね。そうすると、平均の速度\(\bar{v}\)は時刻\(t_1\)における瞬間の速度を表すようになります。
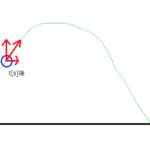
ここで、横軸に時間\(t\)、縦軸に位置\(x\)をとった\(x-t\)グラフを考えましょう。
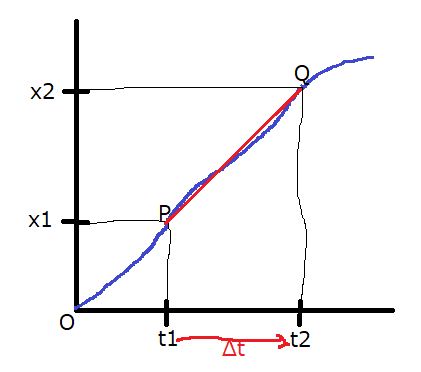
このとき、\(t_1\)~\(t_2\)間の平均の速度\(\bar{v}\)は、点Pと点Qを結ぶ直線の傾きで表せます。\(t_2\)を\(t_1\)に近づけていくと、この直線はグラフと点Pで接する直線に近づいていきます。
点Pで接する直線を点Pにおける接線といいます。つまり、ある時刻における瞬間の速度\(v\)は、\(x-t\)グラフ上でその時刻の点に引いた接線の傾きとして表されます。
この辺については、数学Ⅱ・Ⅲの「微分」の項目で詳しく勉強するので、物理の最初の段階ではサラッと流してて大丈夫です。赤線を引いている部分だけ頭に入れておきましょう。
まとめ
この記事の内容をざっくりまとめておきます。
- 「速さ」に"向き"の情報を足したものを「速度」という。速さはスカラー、速度はベクトルである。
- 物体がどの向きにどれだけ移動したかを表す量を変位という。
- 単位時間当たりの変位を\(\bar{v}\)で表せる。この\(\bar{v}\)を平均の速度という。
- 瞬間の速度\(v\)は、\(x-t\)グラフ上のある時刻の点に引いた接線の傾きとして表される。
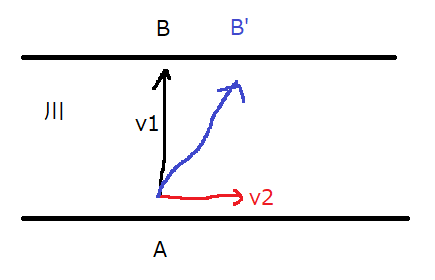
次回は「速度の合成と分解」について扱いたいと思います。ということで、今回の内容はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。