【力学】速度①(等速直線運動など)
今回は、物理について解説していきたいと思います。
今まで数学やIT系の内容が多かったですが、これからは物理についても扱っていこうと思います。化学も扱いたいですが、有機化学とかになると色々ややこしい内容も入ってきてブログで扱うのが難しそうなので、検討中です(笑)
物理の一番基本となる「速度」から取り上げていこうと思います。
速さ
運動する物体の単位時間当たりの移動距離を速さと言います。移動距離を\(x\)、経過時間を\(t\)とすると、速さ\(v\)は次のように表すことができます。
\[v=\frac{\text{移動距離}}{\text{経過時間}}=\frac{x}{t}\text{・・・①}\]
速さの単位は、距離と時間の単位によって変わります。たとえば、距離がメートル(m)、時間が(s)であれば、速さの単位は、メートル毎秒(m/s)となります。
瞬間の速さと平均の速さ
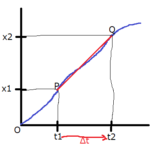
運動する物体の速さは常に一定であることもありますが、基本的にはその瞬間ごとによって速さが異なる場合が多いです。
例えば、自動車を運転する時もそうです。高速道路では一般的に時速100キロメートルが制限速度ですが、ずっと100キロの速さで走り続ける人はまずいないでしょう。90キロで走っていたり100キロを少し超えて102キロで走っていたり…常に100キロの速さで走り続けることは難しいでしょう。このように、運動する物体の速さは、時間とともに変化します。時間とともに変化する速さを瞬間の速さとして扱ったりします。
一方、①式で得られる速さは、平均の速さを表しています。
問題で問われている「速さ」が、平均の速さと瞬間の速さのどちらに該当するかを考えておくようにしましょう。
一直線の道路上にある40m離れた場所へ、80秒かけて歩き、すぐに折り返して10秒で元の位置に戻った。行きと帰りの平均の速さはそれぞれ何m/sか。
行き:0.50m/s 帰り:4.0m/s
等速直線運動
一直線上を一定の速さで進む運動を等速直線運動と言います。
等速直線運動をする物体の進む向きに\(x\)軸をとります。物体が原点\(O\)を通ってからの経過時間を\(t\)[s]とすると、物体の位置\(x\)[m]は\(t\)[s]間の移動距離に等しいです。物体の速さを\(v\)とすると、次の式が成り立ちます。
\[x=vt\text{・・・②}\]
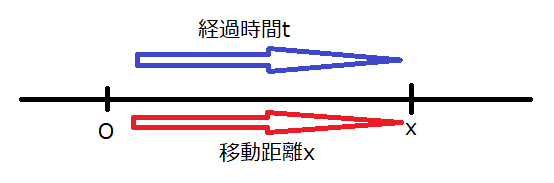
条件:一直線上の運動で、速さ\(v\)が一定
マイケルジャクソンが一定の速さ3.0m/sで進んでいるとき、10秒間で進む距離は何mか。
30m
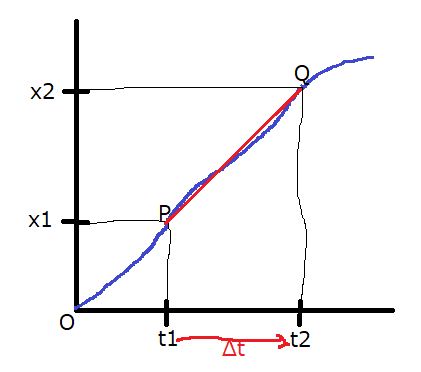
等速直線運動のグラフ
等速直線運動のグラフは、主に2種類存在します。\(x-t\)グラフと\(v-t\)グラフです。それぞれ見ていきましょう。
\(x-t\)グラフ
移動距離\(x\)と経過時間\(t\)との関係を表しているグラフです。このグラフの傾きが速さ\(v\)を表しています。
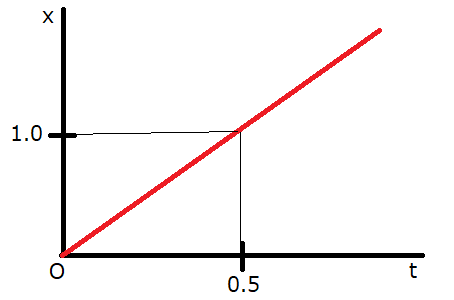
上のグラフは、\(x=2.0t\)という式のグラフです。
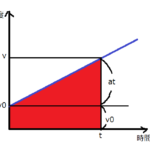
\(v-t\)グラフ
こちらは、速さ\(v\)と経過時間\(t\)との関係を表すグラフです。速さ\(v\)が一定なので、\(t\)軸に平行な直線になります。直線と\(t\)軸間の部分の面積は移動距離\(x\)を表します。
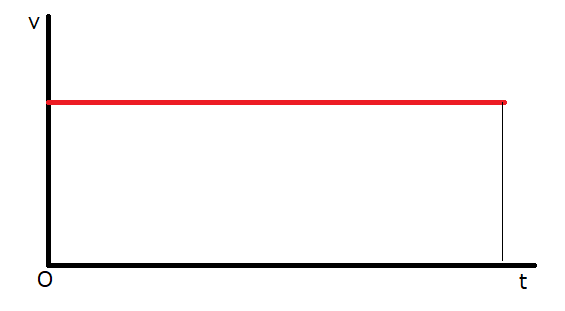
\(v-t\)グラフは速度に変化がない等速直線運動ではグラフの直線が\(t\)軸と平行になりますが、速度が変化するようになると傾きのある直線に変化します。つまり加速度が発生すると、グラフに傾きが付きます。加速度についてはまた後日扱うことにします。
まとめ
- 物体が運動する時の、単位時間あたりの移動距離を速さという。
- 速さには、平均の速さと瞬間の速さがある。
- 一直線上を一定の速さで進む運動を等速直線運動という。
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。