【2次関数】センター試験の問題を解いてみる（2007年度）

2021年5月7日

今回扱う問題のリンクはコチラ↓

問題【前編】

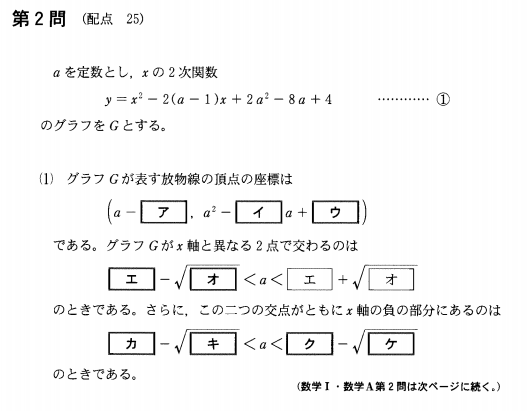
解答（解説）【前編】

ア・イ・ウ

①式を平方完成すると、\(y=\{x-(a-1)\}^2+a^2-6a+3\)

したがって、頂点は

点\((a-1,a^2-6a+3)\)

エ・オ

グラフが\(x\)軸と異なる2点で交わる条件は判別式\(D>0\)です。\(D=b^2-4ac\)より、

\(\{-2(a-1)\}^2-4(2a^2-8a+4)>0\)

これを解くと、

\[3-\sqrt{6}<a<3+\sqrt{6}\]

カ・キ・ク・ケ

「二つの交点がともに\(x\)軸の負の部分である」をグラフに図示してみましょう↓

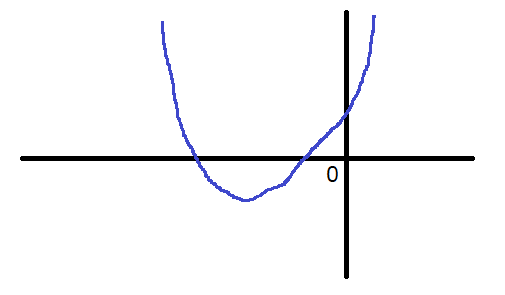
このとき、以下の3つの条件を全て満たしている必要があります。

条件1については、既に範囲を求めました。

\(3-\sqrt{6}<a<3+\sqrt{6}\)でしたね。

条件2については、\(x=0\)をグラフの式に代入して0より大きくなるようにすればよいです。

グラフの式に\(x=0\)を代入すると…\(2a^2-8a+4>0\)

これを解くと、

\(a<2-\sqrt{2},2+\sqrt{2}<a\)

最後に、条件3についてです。

グラフの軸というのは、頂点の\(x\)座標のことです。今回は\(a-1\)です。

\(a-1<0\)すなわち\(a<1\)

以上を全て満たす範囲は…

\[3-\sqrt{6}<a<2-\sqrt{2}\]

問題【後編】

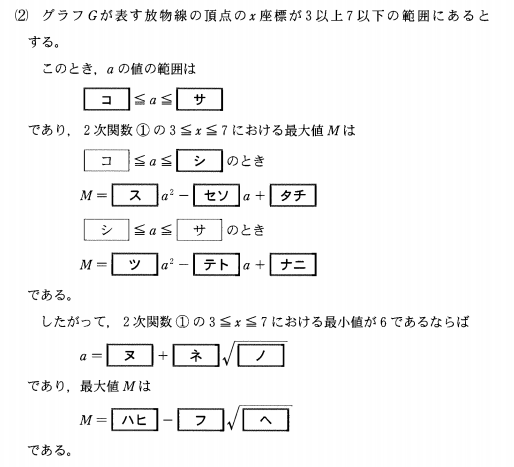
解答（解説）【後編】

コ・サ

頂点の\(x\)座標は\(a-1\)です。これが3以上7以下とあるので、

\(3\text{≦}a-1\text{≦}7\)

これを整理して、

\[4\text{≦}a\text{≦}8\]

シ　ス・セ・ソ・タ・チ

2次関数の下に凸のグラフの場合、基本的に最大値はありません。しかし、定義域が指定される場合は、その範囲の中で最大値を定義することができます。

頂点が最小値なので、頂点から離れれば離れるほど値は大きくなります。したがって、定義域の中で頂点からもっとも離れている、定義域の左端・右端のどちらか・もしくは両方が最大値となります。

定義域の右端が最大値となるとき

この場合は、頂点が定義域の中心より左側にあります。定義域の中心は5ですから、

\(3\text{≦}a-1\text{≦}5\)より、

\[4\text{≦}a\text{≦}6\]

定義域の右端は7です。グラフの式に\(x=7\)を代入すると…

\(y=49-14(a-1)+2a^2-8a+4=2a^2-22a+67\)

したがって、\(4\text{≦}a\text{≦}6\)のとき最大値\(M\)は…

\[M=2a^2-22a+67\]

ツ・テ・ト・ナ・ニ

定義域の左端が最大値となるとき

頂点の軸が5以上7以下である必要があります。このときの\(a\)の範囲は\(5\text{≦}a-1\text{≦}7\)より、\(6\text{≦}a\text{≦}8\)となります。

定義域の左端は\(x=3\)です。グラフの式に\(x=3\)を代入することで最大値\(M\)を求めることができます。

したがって、\(6\text{≦}a\text{≦}8\)のとき、最大値\(M\)の値は

\[M=2a^2-14a+19\]

ヌ・ネ・ノ

頂点の値は\(a^2-6a+3\)です。

\(a^2-6a+3=6\)より、\(a=3\pm2\sqrt{3}\)

\(4\text{≦}a\text{≦}8\)より、

\[a=3+2\sqrt{3}\]

ハ・ヒ・フ・ヘ

\(a=3+2\sqrt{3}\)ですから、\(6\text{≦}a\text{≦}8\)です。

\(2a^2-14a+19\)に\(a=3+2\sqrt{3}\)を代入すると…\(19-4\sqrt{3}\)となります。

したがって、最大値\(M\)は

\[M=19-4\sqrt{3}\]

まとめ

今回の問題を解く上での重要ポイントをまとめてみましょう。

今回はここで終わりです。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。