【2次関数】センター試験の問題を解いてみる(2008年度)
問題のリンクはコチラ↓
Contents
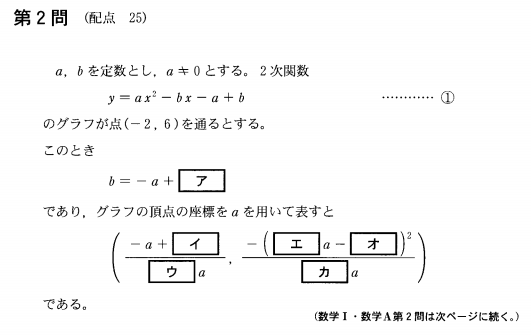
問題【前編】
解答(解説)【前編】
ア
①式に\(x=-2\)、\(y=6\)を代入すると…
\(6=4a+2b-a+b\)より
\[b=-a+2\]
イ・ウ エ・オ・カ
\(b=-a+2\)を①式に代入すると…
\(y=ax^2+(a-2)x-2a+2\)となります。これを平方完成することにより、頂点を導き出すことができます。
すると頂点は
\[\frac{-a+2}{2a},\frac{-(3a-2)^2}{4a}\]
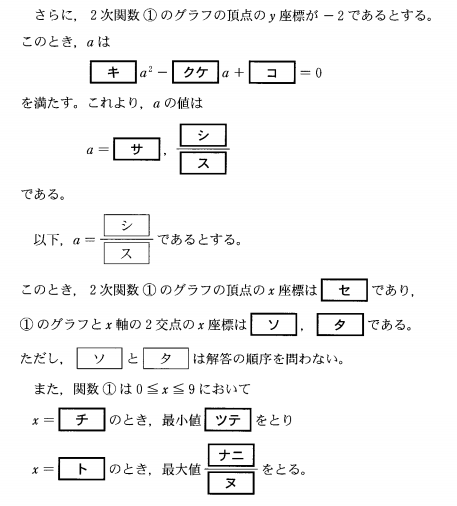
問題【後編】
解答(解説)【後編】
キ・ク・ケ・コ
頂点の\(y\)座標が-2であるので、
\(-2=\frac{-(3a-2)^2}{4a}\)より、
\[9a^2-20a+4=0\]
サ・シ・ス
\(9a^2-20a+4=0\)を解くだけです。
\[a=2,\frac{2}{9}\]
セ
\(a=\frac{2}{9}\)を①式に代入してみましょう。すると…
\(y=\frac{2}{9}x^2-\frac{16}{9}x+\frac{14}{9}\)
これを平方完成すると…
\(y=\frac{2}{9}(x-4)^2-2\)
したがって、頂点の\(x\)座標は4です。
ソ・タ
グラフと\(x\)軸との交点の\(x\)座標は、グラフの式に\(y=0\)を代入することによって求められます。
したがって、\(\frac{2}{9}x^2-\frac{16}{9}x+\frac{14}{9}=0\)より
\[x=1,7\]
チ・ツ・テ
頂点の\(x\)座標は、\(0\text{≦}x\text{≦}9\)を満たしていますので、頂点を最小値とみなすことができます。したがって、\(x=4\)のとき最小値-2をとります。
ト・ナ・ニ・ヌ
グラフの頂点から定義域の左端と右端、どちらが遠いでしょうか。右端ですね。したがって、\(x=9\)の時に最大値をとります。そのときの値は、
\(y=\frac{2}{9}\cdot9^2-\frac{16}{9}\cdot9+\frac{14}{9}\)より、
最大値は\(\frac{32}{9}\)となります。
まとめ
問題を解く上で必要になる重要なポイントをまとめておきます。
以下のグラフ\(f(x)\)は、すべて下に凸のグラフとする。
- グラフ\(f(x)\)が\(x\)軸と交わるときの\(x\)座標は、\(f(x)=0\)とすることで、求められる。
- グラフ\(f(x)\)の最小値は頂点である。しかし、以下の場合には頂点が最小値とはならない。
- 頂点が定義域の左外にあるとき = 定義域の左端で最小値となる
- 頂点が定義域の右外にあるとき = 定義域の右端で最小値となる
- グラフ\(f(x)\)の最大値は基本的には存在しない。無限にグラフは続くからである。しかし、定義域を定めた場合はその中で最大値を取る。以下のような場合に分けられる。
- 頂点が定義域の中心より左にある場合 = 定義域の右端で最大値となる
- 頂点が定義域の中心にある場合 = 定義域の右端と左端の両方で同一の最大値となる
- 頂点が定義域の中心より右にある場合 = 定義域の左端で最大値となる
2020年度の問題から遡って解いてきましたが、難易度がある年を境にどんどん下がっていっている気がします…今回の2008年度の問題なんて、平方完成・2次方程式の変形・2次関数の最大・最小といった基本を理解していれば何も悩むことなく進めることができますから…(笑)
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。
