【2次関数】センター試験の問題を解いてみる（2011年度）

2021年5月3日

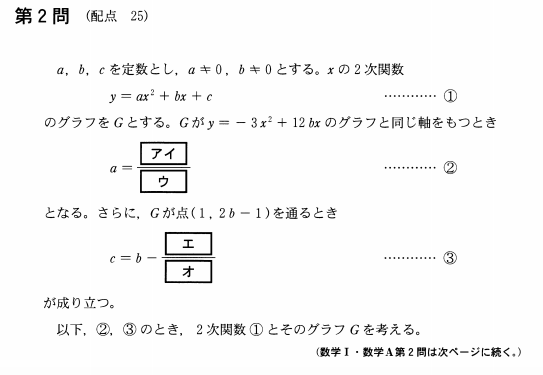
問題【前編】

解説【前編】

ア・イ・ウ

①式を平方完成すると…

\[y=a(x+\frac{b}{2a})^2-\frac{b^2}{4a}+c\]

したがって、①式の軸（頂点の\(x\)座標）は

\[-\frac{b}{2a}\]

です。

同様に、\(y=-3x^2+12bx\)の軸は\(2b\)です。

\(-\frac{b}{2a}=2b\)を解くと…

\[a=\frac{-1}{4}\]

です。

エ・オ

①式に\(a=-\frac{1}{4}\)を代入すると…

\[y=-\frac{1}{4}x^2+bx+c\]

これに\(x=1,y=2b-1\)を代入すると…

\[2b-1=-\frac{1}{4}+b+c\]

式を整理すると…

\[c=b-\frac{3}{4}\]

となります。

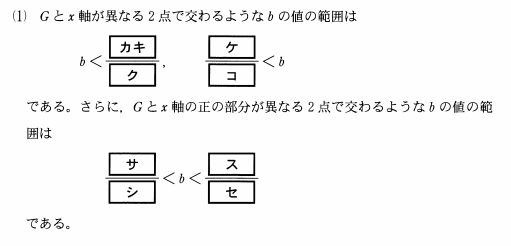
問題【中編】

解説【中編】

カ・キ・ク　ケ・コ

\(x\)軸と異なる2点で交わるということは、判別式\(D>0\)という条件を満たす必要があります。

判別式\(D\)は\(b^2-4ac\)ですから、

\[b^2-4\cdot(-\frac{1}{4})\cdot(b-\frac{3}{4})>0\]

この式を解くと、

\[b<-\frac{3}{2},\frac{1}{2}<b\]

となります。

サ・シ　ス・セ

\(x\)軸の正の部分が異なる2点で交わるためには、3つの条件を満たす必要があります。

条件1は、「異なる2点で交わるため」に必要な条件です。

条件2を満たすことで、\(x\)軸の正と負の両方で交わる可能性を消去できます。（つまり、負の部分で異なる2点で交わる可能性が残っているということ。）

上の赤線部分に書いているような可能性を排除するために必要な条件が条件3です。

条件1に関しては、先程カキクケコの解答の中で出て来ましたね。

\[b<-\frac{3}{2},\frac{1}{2}<b\]

です。

続きまして、条件2についてです。\(G(0)=b-\frac{3}{4}\)ですから、

\[G(0)<0\text{すなわち}b<\frac{3}{4}\]

最後に、条件3についてです。\(G\)の頂点の軸は、\(-\frac{b}{2a}\)でした。先程\(a=-\frac{1}{4}\)だと分かりますので、頂点の軸は、\(2b\)です。したがって、\(2b>0\)つまり\(b>0\)が条件3です。

以上の条件1と条件2と条件3をすべて満たすのは、

\[\frac{1}{2}<b<\frac{3}{4}\]

となります。

問題【後編】

解説【後編】

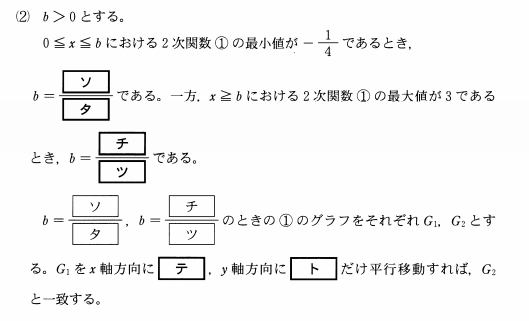
ソ・タ

\(0\text{≦}x\text{≦}b\)において、最小値になる可能性があるのは、\(x=0\)と\(x=b\)です。では、この2つの場合について詳しく見ていきます。

\(x=0\)で最小値となるとき

グラフの式は\(y=-\frac{1}{4}x^2+bx+b-\frac{3}{4}\)です。これに\(x=0\)と\(y=-\frac{1}{4}\)を代入すると…

\(b-\frac{3}{b}=-\frac{1}{4}\)となります。したがって、\(b=\frac{1}{2}\)

グラフの軸は\(x=1\)となり、頂点が\(0\text{≦}x\text{≦}b\)の外に出ます。したがって、最小値は\(x=0\)のときとみなすことができますので、正しいです。

\(x=b\)で最小値となるとき

\(x=0\)のときと同じような流れです。\(y=-\frac{1}{4}x^2+bx+b-\frac{3}{4}\)に\(x=b\)と\(y=-\frac{1}{4}\)を代入すると…

\(-\frac{1}{4}b^2+b^2+b-\frac{3}{4}=-\frac{1}{4}\)

これを解くと、

\[b=\frac{-2\pm\sqrt{10}}{3}\]

となり、\(b>0\)より、

\[b=\frac{-2+\sqrt{10}}{3}\]

グラフの軸は、\(x=\frac{-4+2\sqrt{10}}{3}\)となり、最小値が\(x=0\)になるときと同様に、頂点が定義域の右外にはみ出ます。しかし、最小値が\(x=b\)となるためには頂点が定義域の左外にはみ出なければならないため、矛盾が生じてしまいます。

したがって、今回は最小値は\(x=0\)となり、

\[b=\frac{1}{2}\]

が正解です。

チ・ツ

頂点の軸は\(2b\)ですから、\(x\text{≧}b\)としたときの最大値は頂点となります。

\(y=-\frac{1}{4}x^2+bx+b-\frac{3}{4}\)の頂点は、点\((2b,b^2+b-\frac{3}{4})\)です。

頂点の\(y\)座標は3なので、\(b^2+b-\frac{3}{4}=3\)

これを解くと\(b=\frac{3}{2},-\frac{5}{2}\)です。\(b>0\)より、

\[b=\frac{3}{2}\]

テ　ト

\[G_1=-\frac{1}{4}x^2+\frac{1}{2}x+\frac{1}{2}-\frac{3}{4}\]

\[G_2=-\frac{1}{4}x^2+\frac{3}{2}x+\frac{3}{2}-\frac{3}{4}\]

それぞれの頂点を求めると、\(G_1\)の頂点は点\((1,0)\)であり、\(G_2\)の頂点は\((3,3)\)です。

したがって、\(G_1\)を\(x\)軸方向に2、\(y\)軸方向に3だけ平行移動すれば\(G_2\)と一致します。

まとめ

というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。