【三角関数の入り口】「三平方の定理」を導き出そう!
三平方の定理とは
高校数学を勉強していくうえで避けては通れない重要項目の1つに「三角関数」があります。
三角関数に取り掛かる前に絶対に知っておくべき事があります。
それは
三平方の定理
です。
どんな定理?といいますと、
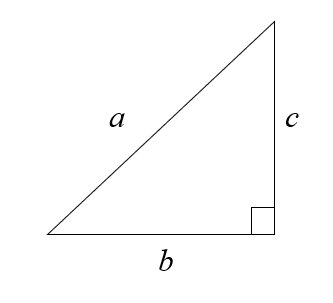
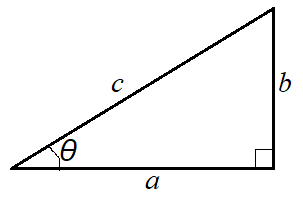
図1のような直角三角形があったとします。
このとき、a・b・cのそれぞれの長さの関係は、
\[a^2=b^2+c^2\]
となります。
↑これが、三平方の定理です。
まあ、これくらいならすぐ覚えられるんですけども。。。
実はこの式、
正方形の面積の求め方と三角形の面積の求め方が分かっていれば、簡単に導き出すことができます。
では、その流れを説明していきます。
長々と説明していますが、もちろん、分かるところはすっ飛ばしてもらって構いません。
三平方の定理の導出
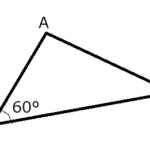
まず、正方形の中に少し小さな正方形を配置した下のような図を考えます。
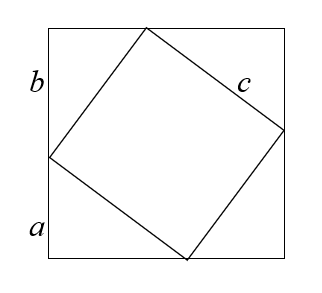
Wordで描いた図なので正確に測ったら正方形じゃないかもしれませんがほっといてください()
図2ですが、三角形4つと小さな正方形の面積を足せば大きな正方形の面積になるのは、言わなくてもわかることだと思います。
ここで、4つの三角形が全部合同で同じ面積になるのはお分かりいただけますか?
三角形の合同について
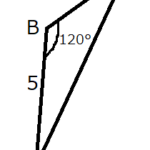
図2の改良版が図3です。左側にある2つの三角形に着目します。
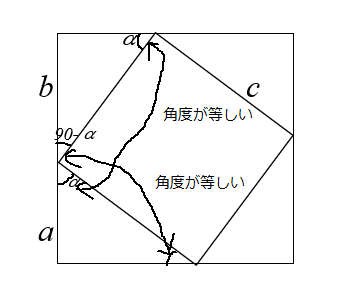
三角形の合同条件は、
- 3つの辺の長さが等しい
- 2つの辺とその間の1つの角度が等しい
- 1つの辺と両端の2つの角度が等しい
でしたね。今回はこの中の3番を使います。では、見ていきましょう。
- 2つの三角形の斜辺は正方形の辺であることから、1つの辺の長さが等しい。
- 図3により、1つの辺と両端の2つの角度が等しい。
よって、2つの三角形は合同です。右の2つの三角形にも同じことが言えます。
したがって、4つの三角形は合同であり、面積が等しいことが分かりました。
ちなみに、上の合同条件のうち、「2つの角度が等しい」理由については、三角形の内角の和は180°である、という規則を使うことで解決できます。
まず、左下の三角形の直角以外の角の角度をαと置きます。
すると、三角形の内角の和は180°であるため、αと直角以外の角の大きさは、
180°- 90°- α、すなわち90°- αです。
続いて左上の三角形の90°- αの導出についてです。
図には90-αと書き込んでますが、ここではまだ分からないものとして、βと置きましょうか。
このβの角度の値を求めます。
直線は180°ですよね。この180°から、直角部分(正方形の内角)の90°と左下の三角形で仮置きしたαを引けばいいので、
β = 180°- 90°- α = 90°- α
したがって、左上の三角形の方においても、90°- αが導き出せます。
この考え方を使えば、左上の三角形のαについても導き出せるはずです。
三平方の定理の導出・仕上げ
では、三平方の定理を導き出していきましょう。
大きい正方形の面積=小さい正方形の面積 + 三角形の面積の和
上の式が成り立つんでしたね。a・b・cを使って当てはめていきましょう。
正方形の面積は、(一辺の長さ×一辺の長さ)なので、大きい正方形の面積は\[(a+b)^2\]ですよね。
続いて、小さい正方形の面積は、\[c^2\]ですね。
最後に、三角形の面積の和は底辺×高さ÷2なので、\[\frac{ab}{2} \times4 = 2ab\]ですね。
必要な情報は揃いました。すべて上の関係式にぶっこみます。
\[(a+b)^2 = c^2 + 2ab\]
上の式を整理します。
\[a^2+2ab+b^2=c^2+2ab\]
\[a^2+b^2=c^2\]
完成しましたね。
まとめ・補足
図1と図2以降では斜辺の値をaからcに変えているためaとcの場所が入れ替わっています。
ですが、式として示していることは全く同じで、
直角三角形では、斜辺以外の2辺の長さの2乗の和=斜辺の2乗の長さ
ということを示しています。
この三平方の定理を理解しておくと、三角関数で出てくる \[\sin^2\theta+\cos^2\theta=1 \] という式が一発で理解できます。
sinとcosについてはまた別の記事で解説しようと思います。
今回はこれで終わりです。
最後まで読んでいただきありがとうございました。