【2次関数】センター試験の問題を解いてみる（2013年度）

2021年5月2日

今回は2013年度のセンター試験の問題（2次関数）の問題を解いていきたいと思います。

今回の問題のリンクはコチラ↓

問題【前編】

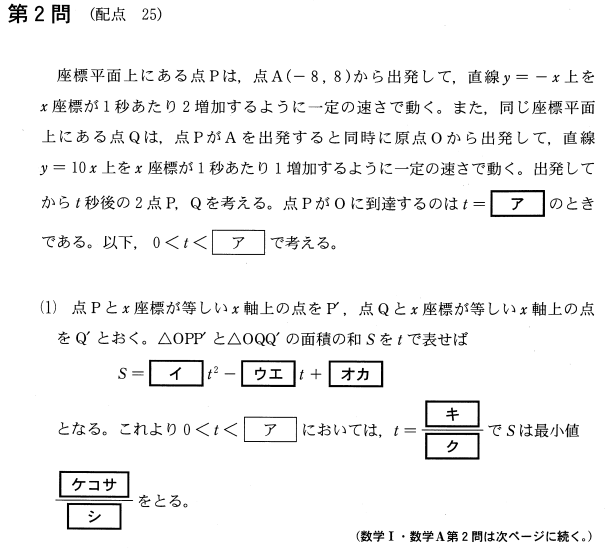
解説【前編】

ア

スタートの時点で\(x\)座標は-8で、1秒につき2ずつ増えていくので、点\(O\)に到達するのは4秒後です。

イ　ウ・エ　オ・カ

面積の和\(S\)についてですが、計算していくと、

\(t=0\)のときに\(S=32\)、\(t=1\)のときに\(S=23\)、\(t=2\)のときに\(S=28\)となります。

2次関数\(S\)の式を、\(S=at^2+bt+c\)として、この式に\(t\)と\(S\)の値を代入していくと、

\[c=32\]

\[a+b=-9\]

\[4a+2b=-4\]

という3つの式から成る連立方程式を作ることができます。この連立方程式を解くと、\(a=7,b=-16,c=32\)となり、求める式は、

\[S=7t^2-16t+32\]

となります。

キ・ク

先程求めた\(S=7t^2-16t+32\)を平方完成すると、頂点は点\((\frac{8}{7},\frac{160}{7})\)となります。\(\frac{8}{7}\)は\(0<t<4\)の範囲の中にあるため、頂点がそのまま最小値となります。

問題【後編】

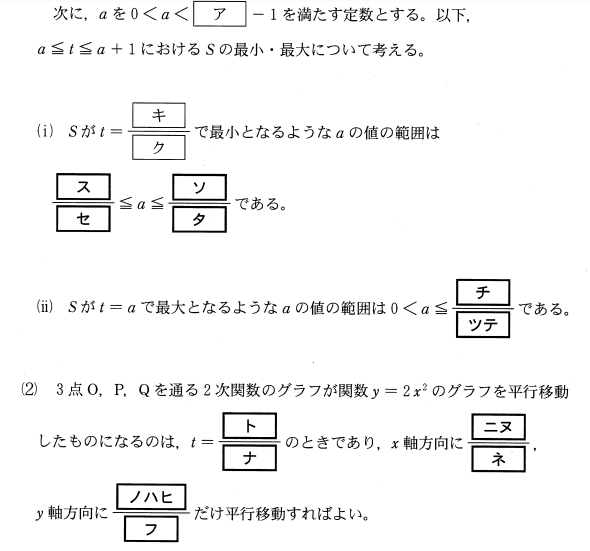
解説【後編】

ス・セ　ソ・タ

頂点が最小値であるためには、定義域の中に頂点がある必要があります。したがって、\(a\text{≦}\frac{8}{7}\text{≦}a+1\)が成立すればよいです。

\[a\text{≦}\frac{8}{7}\]

\[\frac{8}{7}\text{≦}a+1\]

これらを解くと、\(a\)の範囲は

\[\frac{1}{7}\text{≦}a\text{≦}\frac{8}{7}\]

となります。

チ　ツ・テ

定義域の左端が\(a\)であるためには、定義域の中心より右側に頂点があれば良いので…

定義域の中心は\(a+\frac{1}{2}\)です。頂点は\(\frac{8}{7}\)です。したがって…

\(a+\frac{1}{2}\text{≦}\frac{8}{7}\)より、

\[a\text{≦}\frac{9}{14}\]

です。

ただし、問題文の中に\(0<a<3\)という指定があります。これも加味すると…

\[0<a\text{≦}\frac{9}{14}\]

が答えとなります。

ト・ナ

「\(y=2x^2\)を平行移動したもの」とありますので、求める関数の式を\(y=2x^2+ax+b\)とおきます。

\(P\)の座標は、スタート時が\((-8,8)\)です。1秒経つと\(x\)座標の値は2増えて\(y\)座標の値は2減るので、\(P\)の座標は点\((-8+2t,8-2t)\)とおくことができます。

\(Q\)の座標は、スタート時が\((0,0)\)です。1秒経つと\(x\)座標の値が1増えて\(y\)座標の値が10増えるので、\(Q\)の座標は\((t,10t)\)とおくことができます。

そして、点\(O\)は\((0,0)\)です。

以上の内容より、

\[b=0\]

\[2(-8+2t)^2+(-8+2t)a+b=8-2t\]

\[2t^2+at+b=10t\]

という3つの式から成る連立方程式ができます。少し面倒ですが、これを解くと\(t=4,\frac{5}{2}\)、\(a=2,5\)が出てきます。

問題文の冒頭に\(0<t<4\)という指定があるので、\(t=\frac{5}{2}\)、\(a=5\)となります。

したがって、

\[t=\frac{5}{2}\]

となります。

ニ・ヌ・ネ　ノ・ハ・ヒ・フ

関数の式は\(y=2x^2+5x\)ですので、平方完成すると、

\[y=2(x+\frac{5}{4})^2-\frac{25}{8}\]

となります。したがって、\(x\)軸方向に\(-\frac{5}{4}\)、\(y\)軸方向に\(-\frac{25}{8}\)だけ平行移動させたものであることが分かります。

まとめ

今回の問題を解く上での重要ポイントをまとめてみました。

というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。