【2次関数】センター試験の問題を解いてみる（2015年度）

2021年4月29日

今回は2015年度センター試験の2次関数の問題を解いていきます。

問題は↓のサイトから引用しています。

センター試験問題

2015年度大学入試センター試験

Contents

1 問題①
2 解説①
3 問題②
4 解説②
5 まとめ

問題①

問題

解説①

ア・イ

\(y=-x^2+2x+2\)を平方完成すると、\(y=-(x-1)^2+3\)となります。したがって、頂点は点\((1,3)\)です。

ウ・エ

\(y=-x^2+2x+2\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ動かしたグラフが\(f(x)\)とのことです。この\(f(x)\)の式は、

\[f(x)=-\{x-(1-p)\}^2+3+q \text{・・・①}\]となります。

①のグラフは上に凸のグラフですね。上に凸のグラフは定義域の指定がない場合は頂点が最大値となり、最小値は存在しません。ただし、定義域の指定があればその中で最大値と最小値を取ることになります。\(2\text{≦}x\text{≦}4\)の中で最大値が\(f(2)\)ということは、頂点の\(x\)座標が2であるか、もしくは頂点の\(x\)座標が2より小さいと考えることができます。

頂点の\(x\)座標は\(1+p\)です。これが2以下になればいいので、

\(1+p\text{≦}2\)より、\[p\text{≦}1\]が答えです。

オ・カ

最小値が\(f(2)\)ということは、頂点の\(x\)座標が3以上である必要があります。頂点の\(x\)座標が3であれば最小値は\(f(2)\)と\(f(4)\)のときですし、もし3未満であれば最小値は\(f(4)\)のときです。

したがって、\(1+p\text{≧}3\)より、\[p\text{≧}2\]が答えです。

問題②

問題

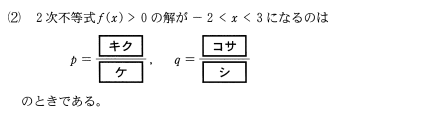
解説②

①式を展開して整理すると、

\[f(x)=-x^2+2(p+1)x-(p+1)^2+3+q \text{・・・②}\]

という式になります。

ここで、問題文の「\(f(x)>0\)の解が\(-2<x<3\)」という部分に着目します。これは言い換えると「\(f(x)=0\)の解が\(x=-2,x=3\)」とも言えるわけです。グラフで示すと、下図のような状態です。

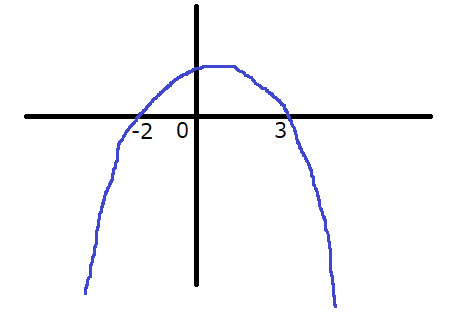
\(x\)軸とグラフが交わるのが\(x=-2\)と\(x=3\)ということです。\(x=-2\)と\(x=3\)を持つ2次方程式を③とすると、③は次のような式になります。

\(-(x+2)(x-3)=0\)より、\[-x^2+x+6=0 \text{・・・③}\]

②と③より、以下のような式を立てることができます。

\[2(p+1)=1 \text{・・・④}\]

\[-(p+1)^2+3+q=6 \text{・・・⑤}\]

④は②と③の1次項、⑤は②と③の定数項に着目して式を立てています。

④と⑤より、\[p=-\frac{1}{2}\]

\[q=\frac{13}{4}\]

となります。

まとめ

今回の問題を解く上で重要なポイントをまとめてみたので、参考にしてみてください。

まとめ

上に凸のグラフでは以下のような性質がある。
- 最小値は定義域の指定がなければ存在しない。定義域が指定されているときは以下の3パターンでそれぞれ最小値の値が異なる。
  1. 頂点が定義域の中心にあるとき
  2. 頂点が定義域の中心より左にあるとき
  3. 頂点が定義域の衷心より右にあるとき
- 最大値は定義域の指定がなければ頂点が該当する。定義域が指定されている場合は以下の2パターンでそれぞれ異なる。
  1. 頂点が定義域の左に外れているとき
  2. 頂点が定義域の右に外れているとき
\(x=a,x=b\)を解にもつ2次方程式は、\((x-a)(x-b)=0\)である。