【2次関数】センター試験の問題を解いてみる（2016年度）

2021年4月28日

今回は、2016年度のセンター試験の数学Ⅰ・A（2次関数の範囲のみ）を解いていきたいと思います。

といっても、この年のセンター試験の問題の中に「これが2次関数の問題！！」っていう決定的なものがなく、代わりに2次関数に近い内容の問題が2つ出題されていました。今回はその2つを解いていこうと思います。

問題のリンク↓

問題①

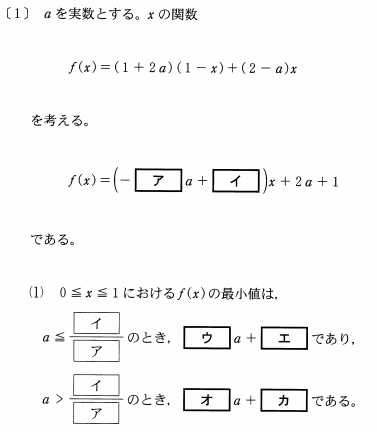
解説①

ア・イ

これは式の変形をするだけですね。展開して\(x\)で括るだけです。答えは、\(-3a+1)x+2a+1\)です。

ウ・エ　オ・カ

この\(f(x)\)は1次関数です。\(a\)という文字が含まれているのでグラフが描けませんが、\(x\)で括った\(-3a+1\)の部分が負の値になればグラフが右下がりになり、正の値になれば右上がりになり、0になれば水平になることが分かりますね。

では、グラフが右上がりの場合から考えてみます。\(-3a+1\)が正であれば右上がりになるんでした。したがって、\(-3a+1>0\)すなわち、\(a<\frac{1}{3}\)のときにグラフは右上がりになります。このときの\(f(x)\)の最小値は…

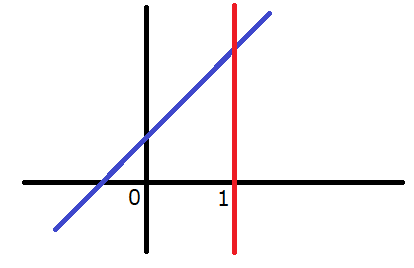
このとき、最小値は\(x=0\)のときですね。\f(0)=2a+1\)ですから、この場合の最小値は\(2a+1\)となります。これがウとエの部分ですね。今回の問題の中では、\(a=\frac{1}{3}\)でグラフが水平の時も最小値は\(2a+1\)になるとみなしていますが、実際は水平の場合は最小値は\(x=0\)でも\(x=1\)でも変わらないです。

続いて、グラフが右下がりの時（\(a>\frac{1}{3}\)のとき）について考えてみましょう。

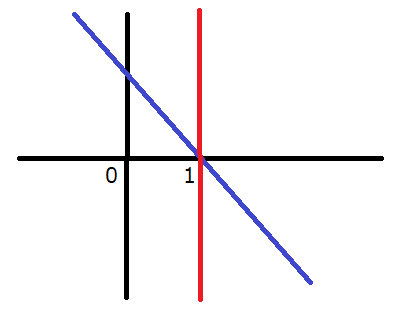
この場合は、最小値は\(x=1\)のときになります。したがって、\(f(1)=-a+2\)となるので、\(-a+2\)が最小値です。

キ・ク　ケ・コ

ウ・エ・オ・カの解答より、この関数では\(0\text{≦}x\text{≦}1\)の場合において、\(-a+2\)と\(2a+1\)のどちらかが最小値で、どちらかが最大値を取ることになります。常に\(f(x)\text{≧}\frac{2(a+2)}{3}\)ということは、\(2a+1\)と\(-a+2\)のどちらも\(\frac{2(a+2)}{3}\)以上の値であればいいわけです。したがって、

①\(2a+1\text{≧}\frac{2(a+2)}{3}\)

②\(-a+2\text{≧}\frac{2(a+2)}{3}\)

①と②を両方満たす範囲が答えです。

①を解くと\(a\text{≧}\frac{1}{4}\)となり、②を解くと\(a\text{≦}\frac{2}{5}\)となるので、

\[\frac{1}{4}\text{≦}a\text{≦}\frac{2}{5}\]

が答えです。

問題②

チ・ツ・テ

\(x^2+(20-a^2)x-20a^2\text{≦}0\)を因数分解すると\((x+20)(x-a^2)\text{≦}0\)となるので、\(-20\text{≦}x\text{≦}a^2\)が答えです。

ト・ナ　ニ

\(x^2+4ax\text{≧}0\)を\(x\)で括ると\(x(x+4a)\text{≧}0\)となるので、答えは\(x\text{≦}-4a,0\text{≦}x\)となります。

ヌ

問題文より、\(a\text{≧}1\)ですね。これを条件Aとします。

チツテとトナニの解答を数直線で整理してみます（ややこしいので、\(a\)が含んでいる箇所は除く）。

\(a^2\)は必ず正の値になるので、0より右側です。したがって、不等式を満たす負の実数が存在するためには、\(-4a\)が-20より右側にある必要があります。したがって、\(-4a\text{≧}-20\)という式が立ちます。これを解くと、\(a\text{≦}5\)となります。

ただし、条件Aを加味する必要があります。したがって、答えは、\(1\text{≦}a\text{≦}5\)となります。

まとめ

今回の問題を解く上で重要なポイントは…

といったところかなと思います。特に難しい知識は必要ないと思いますが、問題文からグラフや数直線をすぐに描けるかどうかがカギとなってくると思います。

ということで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。