【2次関数】センター試験の問題を解いてみる(2019年度)②
2019年度版①はこちらからどうぞ↓
今回は、2019年度の追試の問題を解いていきます。今回の問題はこちらからお借りしました。↓
問題(1)
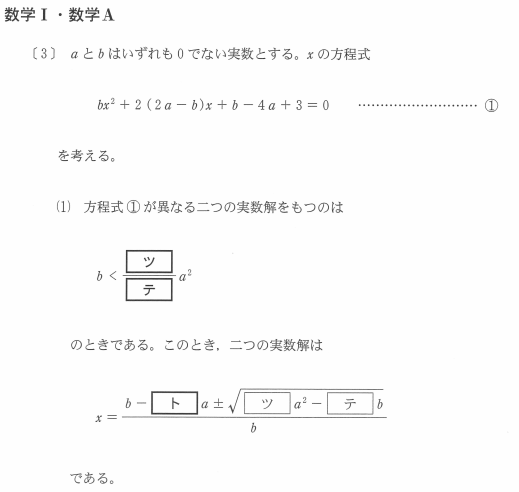
解説(1)
この問題の解決のカギは…判別式です。判別式については過去に解説してますのでよろしければどうぞ↓
異なる二つの実数解をもつということは、判別式\(D>0\)であればいいので、、、
\[\{2(2a-b)\}^2-4b(b-4a+3)>0\]
この式を解くと…
\[b<\frac{4}{3}a^2\]
となり、これがツとテの答えです。
トについてですが、これは解の公式を使います。
解の公式に値を代入すると…
\[x=\frac{2(b-2a)\pm\sqrt{\{2(2a-b)\}^2-4b(b-4a+3)}}{2b}\]
この式を整理すると…
\[x=\frac{b-2a\pm\sqrt{4a^2-3b}}{b}\]
となり、トの答えも出ましたね。
問題(2)

解説(2)
\(b=a^2\)を、方程式に代入しましょう。すると…
\(a^2x^2+2(2a-a^2)x+a^2-4a+3=0\)となります。
異なる2つの実数解をもつということは、先程と同様に\(D>0\)ですね。
\((2a-a^2)^2-a^2(a^2-4a+3)>0\)
この式を整理すると、\(a^2>0\)が出てきます。
つまり、\(a\neq0\)ということですね。この条件を条件Aとして数直線に示したのが下図です。
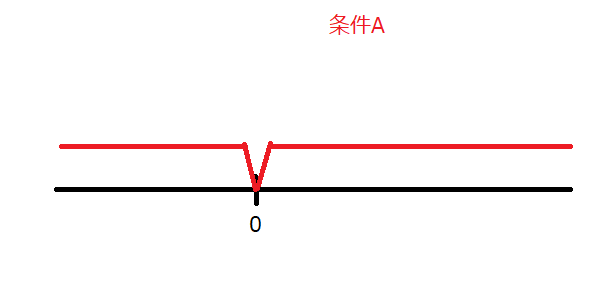
さらに、この2つの解のうち一方が正の解でもう一方が負の解という指定があります。つまり、\(y\)軸とグラフが交わるとき・すなわち\(x=0\)のときの\(y\)の値が負の値を取るということです。なぜこの結論に至るのか、詳しく見ていきましょう。
グラフを描くと分かりやすいため、\(a^2x^2+2(2a-a^2)x+a^2-4a+3=0\)のグラフが上に凸か下に凸かを考えてみます。もし上に凸だった場合、解の2つが正の値と負の値であるためには、\(x\)の値が0だったときの\(y\)の値は正でなくてはなりません。その理由は下の図を見れば分かると思います。
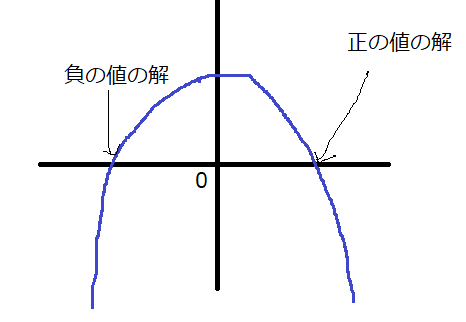
しかし、今回の問題では上に凸ではなく下に凸のグラフになります。なぜかというと、\(x^2\)の係数が正の数だからです。\(a^2x^2+2(2a-a^2)x+a^2-4a+3=0\)の\(x^2\)の係数に着目してください。\(a^2\)ですよね。\(a\)は問題文の最初に記載があるように、実数です。実数は、負の値であろうと正の値であろうと分数であろうとルートを含んでいようと、どんな場合であっても2乗すれば必ず正の数になります。それが実数の性質です。したがって、今回の\(a^2x^2+2(2a-a^2)x+a^2-4a+3=0\)をグラフで示すと下に凸のグラフになるわけです。
したがって、下に凸のグラフで異なる2つの実数解が正の解と負の解であるためには、上に凸のグラフと逆の条件の為、\(x=0\)のときの\(y\)の値が負であればよいということになります(下図参照)。
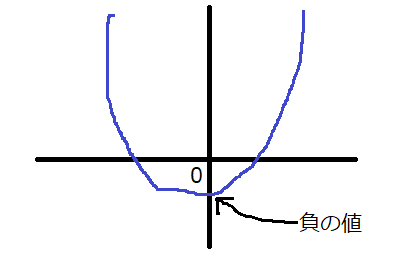
\(x=0\)のときの\(y\)の値が負になる…つまり、グラフの式に\(x=0\)を代入して得られる式が0より小さい値になるようにすればよいです。
\(a^2x^2+2(2a-a^2)x+a^2-4a+3=0\)に\(x=0\)を代入すると…
\(a^2-4a+3\)が得られます。これが0より小さくなればよいので、
\(a^2-4a+3<0\)
したがって、\(1<a<3\)となります。これを条件Bとします。条件Aと条件Bを共に満たすことで「正の解と負の解を持つ」と言えるので…
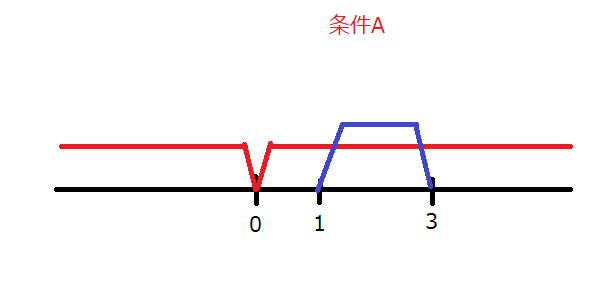
\(1<a<3\)が正解ですね。
と、説明してきましたが、実際には条件Bを満たす時点で異なる2つの実数解を持っているので条件Aは必要ありません(笑)。しかし、次の問題(ヌとネ)を解くためには必要な条件なので、条件Aについて考えたのが無駄になることはありませんので安心してください。
では、最後の問題です。異なる2つの実数解がともに正の数であるための\(a\)の範囲ですね。
これを満たすためには、3つの条件が必要です。
(あ)\(y\)軸と正の値で交わっていること
(い)頂点の\(x\)座標が正の値であること
(う)異なる2つの実数解を持つこと
あ・い・うを満たすことで初めて問題で問われている\(a\)の範囲を決めることができます。どれか1つでも欠けることは許されません。では、どれか1つが欠けた場合を考えてみましょうか。
まず、(あ)についてはすぐに必要な条件だと分かると思います。説明するまでもないかと思います。
では、(い)が欠けるとどうでしょうか。
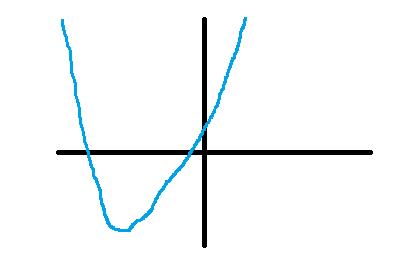
上図のように、異なる2つの負の解をもつようなグラフも描けてしまいます。したがって、(い)は必要な条件です。
では最後に(う)はどうでしょうか。
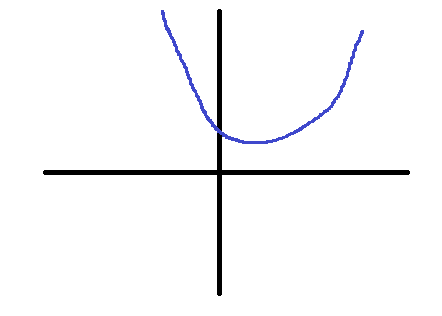
このように、(う)の条件が欠けると、そもそも実数解が存在しないようなグラフが成立してしまう可能性が出てきてしまいます。\(y\)軸と正の値で交わっても、頂点の\(x\)座標が正であっても、実数解が存在しないのであれば問題文の条件から反することになります。
したがって、これら3つ全て必要な条件です。
(あ)については、先程の\(a^2-4a+3\)が逆に0より大きければいいので、
\(a^2-4a+3>0\)したがって、\(a<1\)もしくは\(3<a\)ということになります。これを条件Cとしましょう。
(い)についてですが、関数の式(方程式)を平方完成すればいいですね。
\(a^2x^2+2(2a-a^2)x+a^2-4a+3=0\)を平方完成すると…
\[(x+\frac{2a-a^2}{a})^2-(\frac{2a-a^2}{a^2})^2+a^2-4a+3\]
となるかと思います。頂点の\(x\)座標さえ分かればいいので定数項を整理する必要はないです。
頂点の\(x\)座標は
\[-\frac{2a-a^2}{a}\]すなわち\[\frac{a^2-2a}{a}\]となります。この\(x\)座標が正であるため、
\[\frac{a^2-2a}{a}>0\]
したがって、\(a<0\)または\(2<a\)という答えが出てくるかと思います。これを条件Dとしましょう。
最後に(う)についてですが、これは先程の条件Bのことです。
したがって、条件Bと条件Cと条件Dを全て満たす\(a\)の範囲は…
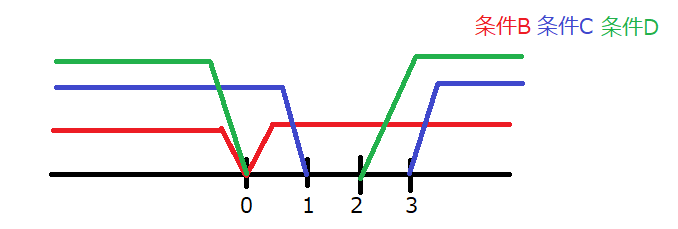
したがって、最後の正解は\(a<0\)と\(3<a\)ですね。
まとめ
今回の問題を攻略するうえで重要なポイントは…
- 下に凸のグラフの場合…正の解と負の解をもつための条件→\(x=0\)のときの\(y\)の値が負である
- 異なる2つの正の実数解をもつための条件
- 判別式\(D>0\)
- \(x=0\)のときの\(y\)の値が正である
- 頂点の\(x\)座標が正である
この辺ですね。私の場合は時間をかけて解くことで正解まで辿り着きました。ただ、センター試験のような短時間でこのレベルの問題を解けと言われるとすごく難しい…(笑)。
特に、今回に関しては(1)がめちゃくちゃ簡単だっただけに(判別式と解の公式を使うだけ)(2)はいろいろと厄介だったように感じました。この問題を数分以内で解けた人はおそらく上位層だと思うので自信を持っていいと思いますね。
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。