【論理回路】論理演算とベン図
Contents
ベン図
今回は「論理演算とベン図」というテーマで解説していこうと思います。
まずは、「ベン図」について掘り下げていきます。ベン図っていっても聞いたことない方や、よく分からないっていう方も多くいらっしゃるかと思います。
簡単に言うと、「集合を表している図」です。高校数学を学んだ経験がある方は、「集合と命題」みたいな単元の中でベン図を扱っているはずなので、覚えていなかったとしても聞き覚えのある単語だと思います。
まずは、そのベン図の種類について考えていきましょう。
論理演算の中で出てくるベン図は、6種類あります。その中でも基本の論理演算が3つあり、まずはこの3つに対応するベン図について理解しましょう。
論理積(AND)
最初に紹介する論理演算は論理積を表す「AND」です。2つの条件があったとき、それを両方満たす場合のみを真とみなします。
例えば、Aの条件が「松本人志を好きな人」で、Bの条件が「浜田雅功を好きな人」というものだとしましょう。すると、AとBを満たす「松本人志と浜田雅功を両方好きな人」のみが真で、それ以外は偽となります。
図で表すと、こんな感じです。
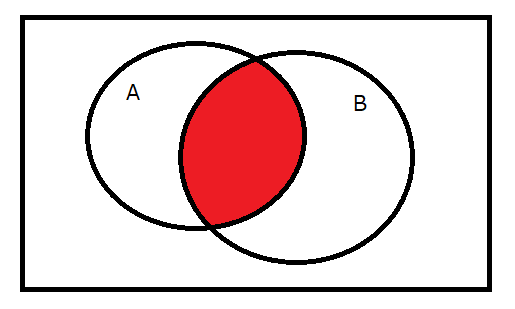
赤の部分のみが「真」です。ちなみにAとBに当てはまる状態を「AかつB」と言ったりします。この「かつ」や「または」は高校数学の「集合と命題」の中でも出てきましたよね。Uって書いたり逆向きのUを書いたり…記号の説明に関してはパソコンで記号を出すのが面倒なので端折ります…(笑)。
論理和(OR)
続いて紹介するのは論理和を表す「OR」です。論理和は、2つある条件の片方・もしくは両方が当てはまる場合に真とみなします。
Aが「松本人志を好きな人」、Bが「浜田雅功を好きな人」であれば、「松本人志を好きな人」「浜田雅功を好きな人」「2人とも好きな人」は真となり、2人とも好きではない人のみが偽となります。
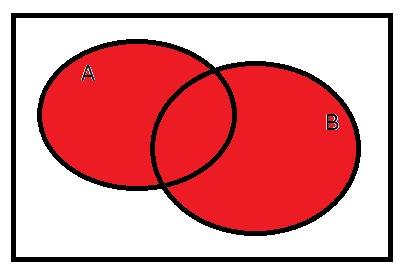
赤で塗ってる部分が真です。ちなみに、AかBのどちらか一方だけでも満たしている場合のことを「AまたはB」と言ったりします。
否定(NOT)
否定は、ある条件を満たさないものを真とみなします。
例えば、ダウンタウンが好きな人というAの条件があったとき、Aの否定(NOT)は下図のような状態です。
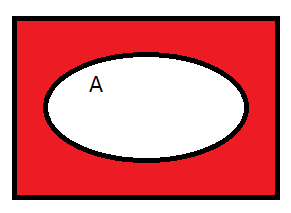
以上の、ANDとORとNOTが基本の論理演算です。これらを複数組み合わせることにより、いろんな論理演算を実現できます。
否定論理積(NAND)
否定論理積とは、論理積(AND)と否定(NOT)を組み合わせたものです。今までの例を使って言うのであれば、「浜田雅功と松本人志を2人とも好きというわけではない」という状態が真とみなされます。ベン図を見るとより理解しやすくなるかと思います。
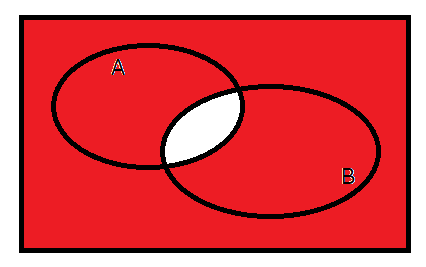
ダウンタウン2人とも好きじゃない場合、松本人志のみ好きな場合、浜田雅功のみ好きな場合はすべて真となり、ダウンタウン2人とも好きという場合のみ偽になります。
否定論理和(NOR)
否定論理和とは、論理和(OR)と否定(NOT)を組み合わせたものです。「浜田雅功も松本人志もどちらとも好きではない」状態が真となります。つまり、ダウンタウンのアンチやダウンタウンに関心がない人のみが真となります(悲しい…笑)。
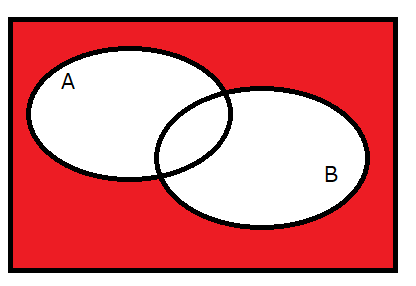
排他的論理和(EORまたはXOR)
排他的論理和というのは、片方のみの条件を満たす場合が真です。つまり、「浜田は好きだけど松本は好きじゃない、松本は好きだけど浜田は好きじゃない」という状態が真となります。これも何か悲しいですね…(笑)。
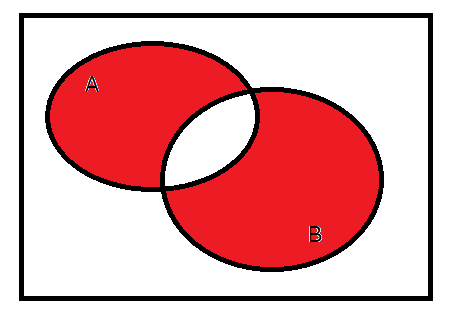
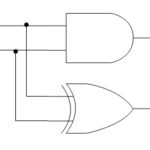
回路
では、ベン図の種類と論理演算の種類を一通り理解したところで、今度は回路図についても理解していきましょう。論理式や真理値表についても一緒に理解しましょう。論理式とは、その状態を表す式のことで、真理値表とは、入力と出力をまとめた表です。
AND
どちらも当てはまる場合のみ真になります。つまり。入力がどちらも1だった場合のみ「1」を出力します。回路図は↓です。
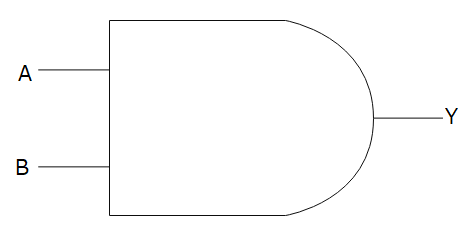
論理式は「A・B=Y」または「AB=Y」という書き方をします。もしくは左辺と右辺を入れ替えて「Y=AB」「Y=A・B」と書いたりもします。真理値表は↓です。
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR
どちらか一方、もしくは両方が1だったときに、「1」を出力します。
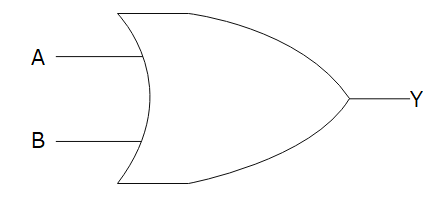
論理式は、「A+B=Y」もしくは「Y=A+B」です。真理値表は↓です。
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
NOT
入力が0なら「1」、入力が1なら「0」を出力します。つまり、入力値を反転させます。
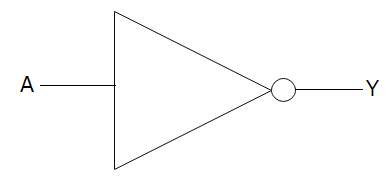
論理式は、以下のように書きます。
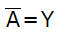
真理値表は他の論理演算と比べてシンプルで、以下の通りです。
| A | Y |
| 0 | 1 |
| 1 | 0 |
NAND
ANDの結果を反転させたような出力になります。したがって、両方1だったら「0」を出力し、それ以外は「1」を出力します。
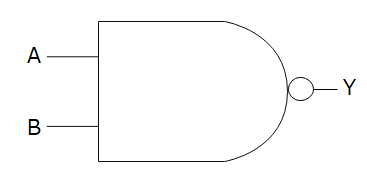
論理式と真理値表は以下の通りです。

| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR
こちらは「OR」を反転したような出力ですので、両方0だった場合のみ「1」を出力し、それ以外は「0」を出力します。
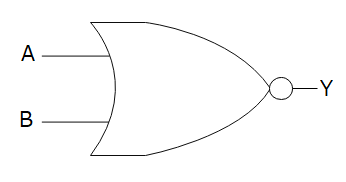
論理式と真理値表は以下のようになります。
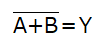
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
EOR または XOR
これは少し特殊な出力でしたね。どちらかが0でどちらかが1の場合は「1」を出力し、どちらも0またはどちらも1だったら「0」を出力します。つまり、AとBの結果が同じであれば0、異なっていれば1を出力します。
回路記号の前に、論理式について理解しましょう。XORの場合は+記号に〇を付けた記号が使われます。
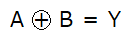
真理値表は以下の通りです。
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
回路記号ですが、よく見る記号は↓の図1です。
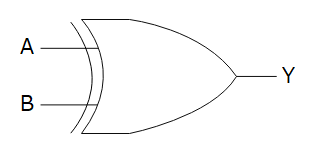
しかし、図2のような形で表すことも可能なので、両方「排他的論理和」であることを理解しておきましょう。
また論理式に関しても、別の表記方法がありますので、こちらも一緒に理解しておきましょう。
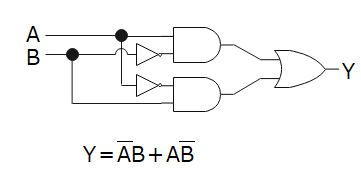
図2の回路記号の仕組みですが、図を見ただけで理解するのは難しいと思います。
理解するコツとしては、論理式を見てみるといいと思います。論理式が「Aの否定とBの論理積」と「AとBの否定の論理積」の論理和という構造であることを理解できれば、あとはそれを各々の記号を使って整理するだけです。
まとめ
今回はベン図と論理演算・論理回路に用いられる記号について解説しました。
論理演算には論理積・論理和・否定という3つの基本的な演算があり、それらを組み合わせた否定論理和・否定論理積・排他的論理和という演算もあります。
というわけで、今回はここで終わりです。最後までお読みいただき、ありがとうございました。