【2次関数】最大値と最小値③
今回は、最大値③ということで、関数式にx以外の文字(a)が含まれている状態で、最大値と最小値を場合分けして考える問題について、解説していきたいと思います。
最大値と最小値①と②は、以下のリンクからどうぞ。
では、早速ですが本題に入っていきましょう!
例題
下に示す関数式 について、(1)と(2)の場合における最小値を求めよ。ただし、\(a\)は定数とする。
\[y=x^2-4ax (0 \text{≦} x \text{≦} 4) \]
(1)\(0\text{≦}a\text{≦}2\)
(2)\(2<a\)
自分で解いてみたい方は、ぜひスクロールを止めてチャレンジしてみてください!
では、解説していきます。
\(y=x^2-4ax\)を変形すると、\(y=(x-2a)^2-4a^2\)になります。
(1)について
\(0\text{≦}a\text{≦}2\)であるから、グラフは下のようになります。
グラフの頂点が\(0\text{≦}x\text{≦}4\)の範囲の中にあります。最小値はグラフの頂点です。
よって、\(y\)は、\(x=2a\)で最小値\(-4a^2\)をとります。
なぜ、頂点が範囲の中に来るのが分かるのか、説明しますね。
\(a\)は0から2の中のいずれかの値であることが(1)の条件です。0から2の中で一番大きな値は2ですよね。このグラフの頂点の座標は、点\((-2a, -4a^2)\)であることは、平方完成の知識があれば分かることです(平方完成については↓からどうぞ)。
\(a\)の値が仮に2だった場合、頂点の\(x\)座標は\(2a\)つまり4です。したがって、最小値を求める範囲の\(0\text{≦}x\text{≦}4\)の中に頂点があることが分かります。
\(a\)の値が仮に0だった場合は、頂点の\(x\)座標は0ですね。つまり、範囲の中に頂点が存在することになります。
\(a\)の値が条件の最大でも最小でも範囲の中に頂点が存在するのであれば、その間(1や0.5など)のすべての数の場合にも同じように範囲内に頂点が存在しますよね。したがって、(1)の場合は、最小値が頂点であると言い切れるのです。
(2)について
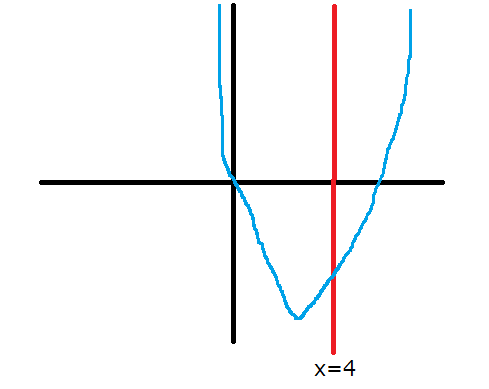
\(2<a\)であるから、グラフは下のようになります。
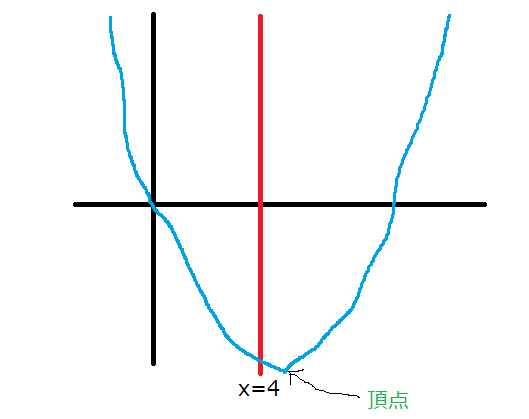
(1)と違って、頂点が\(0\text{≦}x\text{≦}4\)の範囲の外に存在することになります。頂点の\(x\)座標は、\(a\)の値が2より大きくなると、最小値を求めるときの条件である\(0\text{≦}x\text{≦}4\)の右端の4より大きくなってしまいますからね。例えば\(a\)が2.5だったら頂点の\(x\)座標は5なので、頂点は範囲の外に存在することになります。
よって、\(y\)は、\(x=4\)で最小値\(16-16a\)をとります。
まとめ
今回は、場合分けをするときの最小値の求め方について、\(y=x^2-4ax\)を例に解説しました。このような問題を解く大まかな流れは、以下の通りです。
- 関数式を変形する(平方完成)
- \(a\)の範囲を考慮したグラフを描く
- \(x\)の範囲と照らし合わせて最小値がどの値なのかを検討する
やることは多くないのですが、2番が難しいですよね。平方完成は何も難しいことはありませんし、グラフを見て最小値を求めることも簡単です。
この手の問題を解く上で最も重要なのは、\(a\)についてなぜ場合分けを行うのかを理解することだと思います。先程の例題では\(0\text{≦}a\text{≦}2\)と\(2<a\)に場合分けをしましたが、場合分けを行う目的は、\(a\)の値の範囲によって最小値が変わるからです。
今回は、問題の中で場合分けがされていましたが、難しい問題になると、場合分けを自分で行うものがほとんどです。こういった問題を早く解くためのコツは、関数式を見たら、定数値(\(a\)であることが多い)について分析をして、どの値を境に最小値が変化するかを見極めることですね。
応用例題
では、最後に先程の例題をもう少しグレードアップさせたものを出題しておくので、ぜひ解いてみてください。解答も下の方に載せてます。
関数\(y=x^2-4ax(0\text{≦}x\text{≦}4)\)の最小値を\(m\)、最大値を\(M\)とする。\(m\)と\(M\)の値を求めよ。ただし、\(a\)は定数とする。
頂点が範囲の外で左側にあるのか、範囲の中にあるのか、範囲の外で右側にあるのか…
頂点が範囲の中にある場合でも、最大値と最小値は常に同じでしょうか?それとも…?
合計で何パターンの場合分けが生じるのか考えてみてください。
グラフはスペースを大きく取ってしまうので省略します。ぜひご自身で描いてみてください。)
(1)\(2a<0\)すなわち\(a<0\)のとき(頂点が範囲の外)
\(m=0\)(\(x=0\)のとき)、\(M=16-16a\)(\(x=4\)のとき)
(2)\(0\text{≦}2a<2\)すなわち\(0\text{≦}a<1\)のとき(頂点が範囲の中で左寄り)
\(m=-4a^2\)(\(x=2a\)のとき)、\(M=16-16a\)(\(x=4\)のとき)
(3)\(2a=2\)すなわち\(a=1\)のとき(頂点が範囲の真ん中)
\(m=-4\)(\(x=2\)のとき)、\(M=0\)(\(x=0,4\)のとき)
(4)\(2<2a\text{≦}4\)すなわち\(1<a\text{≦2\)のとき(頂点が範囲の中で右寄り)
\(m=-4a^2\)(\(x=2a\)のとき)、\(M=0\)(\(x=0\)のとき)
(5)\(4<2a\)すなわち\(2<a\)のとき(頂点が範囲の外)
\(m=16-16a\)(\(x=4\)のとき)、\(M=0\)(\(x=0\)のとき)
いかがだったでしょうか。どこで場合分けをすればいいのかが分かっていれば、グラフを描いたらすぐに最小値と最大値が分かりますよ。
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。