【浮動小数点数】IEEE754とは
浮動小数点数の形式のうち、ごくシンプルな32ビットの形式例については過去の記事で扱いました。
今回は、別の形式である「IEEE754」という形式を紹介したいと思います。
Contents
IEEE
本題に入る前に、まずIEEEについて少し説明したいと思います。ITに関する勉強をしていると、この4文字のアルファベットをしょっちゅう見かけます。Wi-Fiの規格名にも付いていたりします。では、IEEEとは何かというと、米国電子電機技術者協会のことです。これだけ言われてもよく分からないですよね。
IEEEは、アメリカに本部を置いている、電気・情報工学分野の学術研究団体、技術標準化機関のことです。1963年に発足されました。2018年時点において世界最大の学術研究団体であり、423000人以上の会員がいるそうです。42万人ってどのくらいの数かと言いますと、私が現在住んでいる長崎市の人口と同じくらいです(ちなみに長崎市の人口は2015年時点で42.95万人)。
IEEEについてもっと詳しく知りたい方は、ご自身で調べてみてください。Wikipediaのリンクは↓に貼っておきます。
IEEE754
では今回の本題に入りましょう。IEEE754とは、IEEEによって規格された浮動小数点数の形式です。32ビットや64ビット、128ビットといった形式がありますが、今回はその中の32ビットの形式について紹介します。
先程紹介した記事で説明した32ビットの形式とは異なる部分があります。ビット数の内訳や指数部の表し方、正規化の方法などが異なるので注意しましょう。
ビット数の内訳
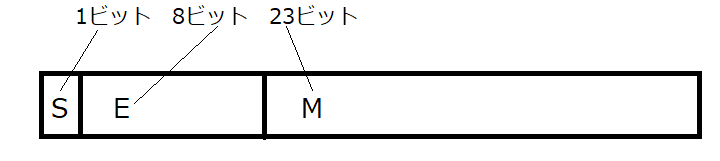
Sは仮数部の符号を表します。1ビットです。
Eは指数部を表します。こちらは8ビットであり、以前の例とは異なる部分です。どうして8ビット使えるのかは後程分かります。
Mは仮数部を表します。こちらは23ビットであり、以前の例より1ビット少ないです。
仮数部の表し方
以前の例では、正規化するときに、0.M(小数第一位が1になる)という表記にしていました。しかし、今回のIEEE754の形式では1.Mという表記で扱います。したがって、0.11×10-1という表記ではなく、1.1×10-2という表記になります。つまり、0.Mの形から1.Mの形にすることで、1ビット多く表現することが可能になります。
バイアス
IEEE754による形式では、指数部の表記にバイアス表現をします。バイアスには、ある数に特定の数を足して嵩上げするという意味があります。補数を使って-127~128という風に指数を表現するのではなく、バイアス表現ではこれらの値に127を足して0~255で表記します。この方が、大小関係が分かりやすいためにこういう表記が行われます。
実際に表現してみよう
では、実際にIEEE754形式で表現してみましょう。以前と同様に、10進数の0.1875を例に説明していきます。
2進数に変換
0.1875を2進数に変換してみましょう。0.0011になりますね。
正規化
続いて、正規化を行います。1.Mの形で表記するので、1.1×10ー3になります。
符号と仮数と指数の値の抜き出し
仮数部の符号はすぐ分かりますね。0です。
続いて、仮数部の値はどうでしょうか。1ですね。
気を付けるべきなのは、指数部の値(8ビット)です。-3なので補数表記で11111101と表記しそうになりますが、そうではありません。バイアス表現をしなければいけないため、+127を行って124を2進数表記します。したがって、01111100になるかと思います。
はめ込み
では、すべての準備が整ったので、最後に形式通りに各値をはめ込みましょう。すると…
| 0 | 01111100 | 10000000000000000000000 |
IEEE754形式で表現することができました。
まとめ
今回は、IEEE754形式による浮動小数点数の表現について解説しました。
IEEE754形式では、指数部を8ビット、仮数部を23ビットで表現する点が特徴です。
指数部の表現にはバイアス表現を用いるので気を付けましょう。
仮数部は1.Mの形式に正規化を行います。
ということで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。