【2次関数】最大値と最小値②

2021年4月12日

今回は以下の内容について解説します。

このタイプの問題は、場合分けを行うことがないため、そんなに難しくも複雑でもないです（笑）。

ちなみに、定義域についてよく分かっていない方は、こちらの記事も参考にしてみてください。

例題

では、解説していきます。

解説の前に自分で解いてみたい！という方は、ぜひここでスクロールを一旦止めて解いてみてください！

（１）について

手順1：平方完成して頂点の座標を求める

まず、頂点を知る必要があります。平方完成しましょう。平方完成については別の記事で解説しています。

y = x²-2x+cを平方完成すると…

y = (x-1)²-1+c という形になるかと思います。したがって、頂点の座標は（1, -1+c）であることが分かります。

ここで疑問に思う方がいると思います。

「いや、頂点のxの値は分かったけど、yの値は分からないやん？」と。

それは当然です。cという不確定の値が式に入っている以上、yの値は分からなくて当然です。このyの値を決めるために、問題文の中で定義域の指定があるのです。段階を踏めば必ずcの値は求められます。

手順2：グラフを書く

ここで気を付けるのは、正確なグラフは書かなくていいということです。cの値が分からない以上、グラフを正確に書くのは不可能です。頂点のxの値が1であるということと、下に凸のグラフであるという2つのポイントを押さえて、グラフのおおよその形を描ければOKです。

このグラフを書く目的は、定義域の(1≦x≦5)の範囲の中でどこで最小値をとってどこで最大値を取るか？を読み取ることです。グラフが美しく書きたくなるのは分かりますが、あくまでも目的は最大値と最小値をどこで取るかを判断することです。

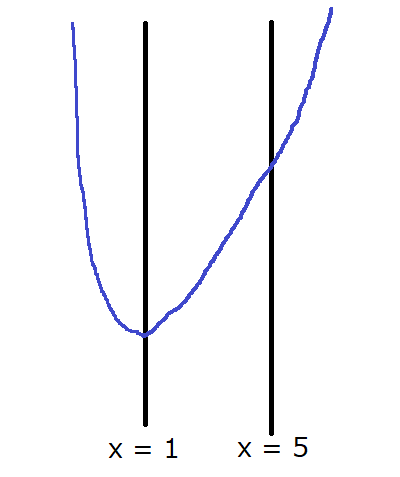
上図のようなグラフになるかと思います。このくらい雑で大丈夫です（笑）。では、手順3に進みましょう。

手順3：最大値をどこで取るかを判断し、式にxの値を代入

上の図を見てください。x=1～5の中で、最大値を取る部分はどこでしょうか。間違いなく、x=5のときですよね。それが分かれば、先程の関数の式y = x²-2x+cにx=5を代入します。すると…

y = 25-10+c = 6

15 + c = 6

したがって、c = -9

cを求めることができましたね。グラフの形さえ描けてしまえば、何も難しいことはないですよね。

では、もう1つの問題も解いてしまいましょう。

（２）について

こちらの問題も、（１）と同様の手順で解くことができます。

手順1：平方完成をして頂点を求める

y=-x²-4x+cを平方完成すると、y = -(x+2)²+4+cとなるから、頂点は、点(-2, 4 + c)です。

手順2：グラフを描く

この関数のグラフは下図です。

手順3：関数式と最小値を取るxの値を用いてcを求める

上のグラフより、0≦x≦4の中で最小値を取るのはx=4のときです。

関数式y=-x²-4x+cにx=4を代入すると…

y = -16-16+c = -32 + c

最小値は-2であるから、

-32 + c = -2　したがってc = 30

類題

実際に問題を解いた方が理解が深まると思うので、いくつか問題を作りました。

ぜひ、理解を深めるために役立ててください！

ちなみに、答えは（１）c = -21、（２）c = 2、（３）c = 3です。

まとめ

今回は、2次関数において定義域が指定されているときの最大値・最小値の求め方について解説しました。

平方完成して、グラフを描いて、最大値・最小値をとるxの値を関数式に代入、という3つの手順で定数の値を導き出すことができます。

---

というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。