【2次関数】最大値と最小値①
今回は2次関数の最大値と最小値について考えていきたいと思います。定義域の制限がある場合とない場合・2次式の係数が+か−かなどが判断材料になります。詳しく見ていきましょう。
定義域の制限がない場合
定義域というのは、(〇 ≦ x ≦ 〇)というような、xの値の範囲のことです。xの上限と下限が設定されている状態のことを、定義域の制限があるとみなします。
定義域の制限がない場合というのは、関数の式の2次項の符号によって最大値と最小値があるかどうかが決まります。
たとえば、y = 2x²+4x+3という式があるとします。この場合、2次項の係数は2であり、符号は+ですね。グラフを書いてみましょう。
平方完成すると、y = 2(x+1)² + 1です。頂点は点(-1, 1)です。平方完成についてはコチラ↓をどうぞ。
グラフを書いてみると…

このような形になります。このグラフを見ると、頂点が最小値であることが分かりますね。では最大値はどうでしょうか。たとえば、xの値を3までという風に定義域に制限をかければ最大値は決まるのですが、定義域の制限がない状態では最大値はありません。
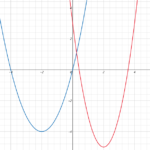
では、2次項の符号が−のときはどうでしょう。y = -x²+6x-8を考えてみましょうか。先程と同様に、平方完成するとy = -(x – 3)² + 1となり、頂点は点(3, 1)です。グラフを書いてみると…

このような形になります。このグラフの最大値は、頂点ですよね。つまり、x = 3のときに最大値1になります。
一方、最小値の方はどうでしょうか。定義域に制限をかけない限り存在しませんよね。
つまり、定義域の制限がない場合の最大値と最小値について整理すると、以下のようになります。
2次関数 y = a(x – p)²+qの最大値と最小値は以下の通りである。
a > 0のとき。x = pで最小値qをとる。最大値はない。
a < 0のとき、x = pで最大値qをとる。最小値はない。
定義域の制限がある場合
定義域の範囲に頂点が含まれているとき
定義域に制限をかけてみましょう。たとえば、y = x² – 4x + 3という式があるとします。この時、定義域を(0 ≦ x ≦ 3)に制限した場合、最大値と最小値がどうなるかを考えましょう。
y = x² – 4x + 3を平方完成した式はy = (x – 2)² + 1です。頂点は、点(2, 1)です。この関数のグラフは下図です。
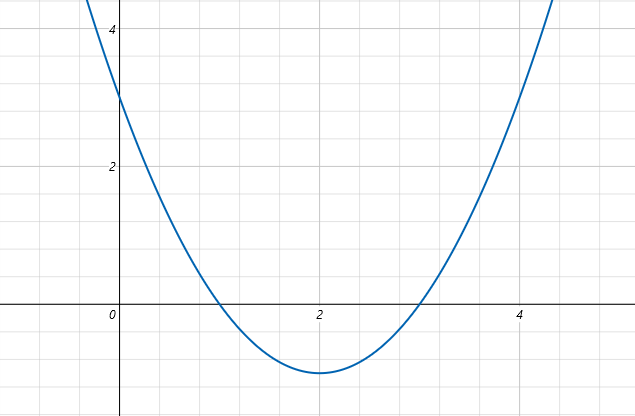
上のグラフに定義域の(0 ≦ x ≦ 3)の範囲を分かりやすく加工をしたのが下のグラフです。

x = 0~3の範囲を黒線でなぞってみました。この黒線の範囲が、定義域の範囲です。この黒線の範囲の中で最大値はどこでしょうか。x = 0のときのy = 3が最大値ではないでしょうか。
一方、最小値はどこかと言いますと、x = 2のときのy = -1ですよね。つまり頂点です。このように、定義域の範囲の中に頂点が含まれているときは最小値を求めるのが楽です(a < 0のときは頂点が最大値)。
定義域の範囲の頂点が含まれていないとき
続いて、y = -2x²-4x -3 (0 ≦ x ≦ 1)について考えましょう。
平方完成した式は、y = -2(x + 1)²-1であるから、頂点は点(-1, -1)です。この関数のグラフは下図です。

定義域は0 ≦ x ≦ 1です。この範囲の中で最大値と最小値は次のようになります。x = 0のとき最大値-3をとり、x = 1のとき最小値-9をとります。
まとめ
今回は2次関数の最大値と最小値について解説しました。
2次関数y = a(x – p)²+qの場合、aが負であれば最大値は頂点で最小値は存在せず、aが正であれば最小値は頂点であり最大値は存在しません。
定義域の制限がある場合は、関数のグラフを書いてから定義域の範囲を見ることで最大値と最小値が分かります。このとき最大値及び最小値が頂点と一致するかどうかは頂点が定義域の範囲にあるかどうかで決まります。
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。