【基本情報】固定小数点数と浮動小数点数
コンピュータの内部では10進数ではなく2進数で表現されます。
今回は、小数の表し方について解説します。コンピュータは、固定小数点数と浮動小数点数という2つの表し方を使います。
Contents
固定小数点数とは
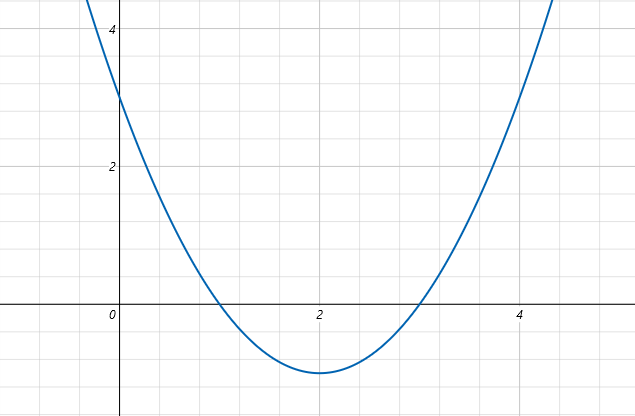
固定小数点数は、ビット列のどの位置に小数点があるかを決めて小数を扱う表現方法です。
例えば、6ビット目と7ビット目の間に小数点があるという風に決めれば、「000000.00」や「111111.11」のような表記になりますし、4ビット目と5ビット目の間に小数点があるという風に決めれば、「0000.0000」や「1111.1111」といった表記になります。
固定小数点数で表せる整数の範囲は以下の通りです。
| 2進数 | 10進数 | |
| 最小 | 00000000 | 0 |
| 00000001 | 1 | |
| … | … | |
| 11111110 | 254 | |
| 最大 | 11111111 | 255 |
符号なしの場合、8ビットの固定小数点数では、0から255まで表すことができます。nビットで表現できる範囲は0~2ⁿ-1です。
| 2進数 | 10進数 | |
| 最小 | 10000000 | -128 |
| 10000001 | -127 | |
| … | … | |
| 0 | 0 | |
| … | … | |
| 01111110 | +126 | |
| 最大 | 01111111 | +127 |
符号ありの場合は-128から127までを表すことができます。ここで気を付けることは最上位ビットが符号ビットであること、負の数は補数表現で表していることです。
補数についてよく理解できていない方は↓の記事を参考にしてみてください。
符号あり8ビットの固定小数点数では、nビットで表現できる範囲は、-2ⁿ⁻¹~2ⁿ⁻¹-1です。
符号なし:0~2ⁿ-1
符号あり:-2ⁿ⁻¹~2ⁿ⁻¹-1
浮動小数点数とは
浮動小数点数は、指数表記を用いて数値を扱います。
指数表記って、高校生の化学の授業でよく出てきたような記憶があります。炭素12gに含まれる原子の個数が6.0×10²³個であり、この数のことをアボガドロ数と呼んでよく使っていました。おそらくこの記事を読んでいる方は高校化学は勉強した経験があるはずなので、見覚えあるはず…(笑)。アボガドロ数について解説する暇はないので、詳しく知りたい方のためにWikipediaのリンク張っておきますね(笑)。
先程のアボガドロ数の10の右上に出てくる23という数字。こいつのことを指数といいます。この例の場合、6.0のことを仮数、10のことを基数といいます。

仮数の前には通常、符号が付きます。+か-のどちらかですね。
馴染みのある10進数で用語の説明をしましたが、実際にコンピュータが扱うのは2進数なので、当然基数は2になります。
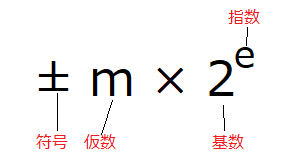
コンピュータで数字を扱う場合は必ず2進数です。なので、基数が「2」から変わることはありません。8進数を扱うときも16進数を扱うときも内部の処理は2進数です。コンピュータは可変部分(符号・仮数・指数)の値をビットに割り当てて数を表現します。
浮動小数点数の正規化について
ある数を表すとき、「指数と仮数の組み合わせ」は無数に存在します。先程の6.0×10²³であれば、60×10²²と表すこともできますし、0.6×10²⁴と表すことも可能です。どの表現方法が間違いということでもありません。
しかし、限られたビット数の中でより多くの情報を保持しようと思うと、より適した表記にする必要があります。適した表記をするために小数点の位置を調整する必要があります。この調整の操作のことを正規化と呼びます。この正規化の考え方は基本情報技術者試験では頻出の内容なので、もし受験するのであれば必ず理解しましょう。
浮動小数点数形式で表してみよう
32ビット形式の表記について説明していきます。他にもIEEE754形式もあるのですが、今回は割愛します。
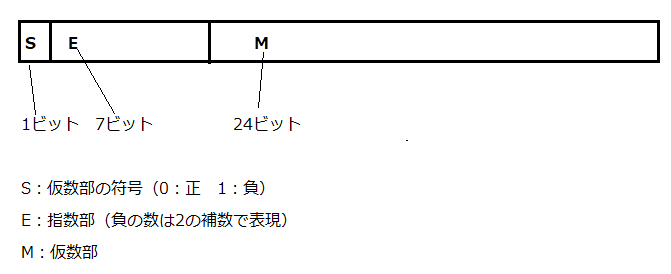
32ビット形式では、全体が32ビットで構成されています。指数部の値が負の数の場合は2の補数を使って表します。仮数部には正規化後の小数部が入ります。(0.11であれば11がMに該当する)
32ビット形式の構造が分かったところで、0.1875を浮動小数点数表記で表現してみましょう。
浮動小数点数で表記する手順は、以下の通りです。
- 10進数表記を2進数表記に変換
- 小数第一位に0以外の数が来るように正規化する
- 符号と仮数と指数の値をそれぞれ抜き出す
- 32ビット形式にはめ込む
10進数表記を2進数表記に変換
0.1875を2進数表記に変換します。

0.1875を手順通りに2進数表記に変換すると、0.0011になります。
正規化
0.0011を正規化します。小数点第一位が0以外(つまり1)にします(2進数であることに注意)。今回は小数第一位と第二位が0なので、2を2回かけて、0.11×2⁻²と表記します(指数部の数は正規化の中で2をかけた回数を入れます)。
符号と仮数と指数を抜き出す
0.11×2⁻²が正規化した結果でしたね。この中から符号と仮数と指数を抜き出します。
符号は正の数なので0ですね。
指数は-2なので、1111110(補数表現に直して7ビット表記)です。
仮数は11です。
はめ込み
最後に最後に、指定された形式に各値をはめ込みます。
| 0 | 1111110 | 110000000000000000000000 |
仮数部は、今回は3桁目以降は存在しないので0で埋めます。
まとめ
今回は、固定小数点数と浮動小数点数について解説しました。
固定小数点数は、小数点の位置を決めてしまう方法です。
浮動小数点数は、指数表記を用いて数値を扱います。浮動小数点数形式では正規化という桁合わせなどの処理を経て表記を行います。
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。