【2次関数】平方完成って何?について解説します
高校数学の中で重要な項目の一つとして挙げられる2次関数。その中で、耳にタコができるほど多くの場面で遭遇するのが「平方完成」という言葉。
平方完成って何?っていうところから、丁寧に解説していきたいと思います。
平方完成とは
「平方完成」とはそもそも何でしょうか。ちなみに、Wikipediaでは以下のように説明されています。
平方完成とは、二次式を式変形して
https://ja.wikipedia.org/wiki/%E5%B9%B3%E6%96%B9%E5%AE%8C%E6%88%90の形を作り、一次の項を見かけ上なくすことである。
平方完成を行うと、必ず、
\[a(x – p)^2 + q \]
という形になり、たしかに一次の項はなくなりますね。
では、なぜ平方完成を行う必要があるのでしょうか。
平方完成を行う意味
平方完成がどういうものなのかを理解できましたね。では、平方完成は何のために行うのでしょうか。
それは、グラフの頂点を求めるためです。
\[y = a (x – p)^2 + q \]
という式があったときに、頂点は、点(p, q)であるという風に定義されています。
頂点の定義についての説明
具体的な例を考えてみましょう。
\[ y = 2(x – 3)^2 + 1 \]
という関数があったとしましょう。この関数の式を①式とします。関数のグラフの出力値について考えてみます。
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| 2(x-3)²+1 | … | 51 | 33 | 19 | 9 | 3 | 1 | 3 | … |
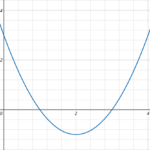
①式の出力値の変化を見ると、x=3のときy=1であり、このときが頂点であることが分かります。ちなみにグラフを描くとこのような感じです。

この点(3,1)はわざわざxに値を代入しなくても、関数の式を見れば分かりますよね?このように、平方完成をした式があれば、入力値を与えたり出力値を求めることなく、頂点が求められます。したがって、以下のように定義できるわけなんです。
y=a(x-p)²+qのグラフの頂点は、点(p, q)である。
平方完成の方法
平方完成をするとどのような形の式になるのか、平方完成を行う意味を理解できましたね。では、その平方完成はどのように行えばいいのか、解説していきます。
y=x²+4xという式を平方完成していきましょう。
1次式の係数に着目しましょう。この場合は「4」ですね。
続いて、係数の半分の数を求めます。この4の半分の数は2です。
平方完成が終了すると(x+〇)² + △の形になります。〇の部分に先程求めた一次式の係数の半分の値を入れます。今回であれば、(x + 2)²になりますね。
この式を展開するとx²+4x+4になってしまい、x²+4xと比べると「+4」が邪魔ですね。
したがって、この差を打ち消すために「-4」を△の部分に入れてやります。そうすると、y = (x + 2)²-4になりますね。これで平方完成が終了です。
では、もう1度別の式を平方完成してみましょう。
y=2x²-8x+3という式を平方完成してみましょう。2次式の係数に着目してください。2次式の係数が1であればそのまま平方完成を行えますが、2次式に2以上の係数がある場合は少し変形します。
y = 2(x²- 4x) + 3という風に、2次式の係数で括ることで平方完成を進めていくことができます。x²-4xを平方完成すると、(x – 2)² – 4になります。これをx²-4xの部分に代入してやります。
すると、y = 2 {(x – 2)² – 4} + 3となります。-4を{}の外に出します。
すると、y = 2{(x – 2)²} – 5となります。{}を外すことにより、y = 2(x – 2)² – 5となり、ここで平方完成が終了します。
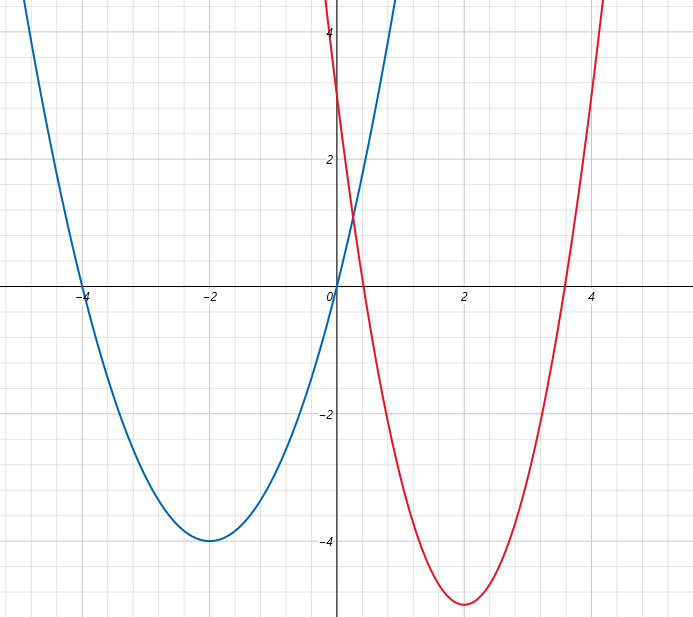
ちなみに、先程のy = x²+4xとy = 2x²-8x+3をグラフで表すと、このような感じになります。
まとめ
今回は、2次関数の平方完成について説明しました。
平方完成を行うことでグラフの頂点を求めることができます。
平方関数を行う上で注意することは、2次式の係数です。係数が2以上であれば、少し面倒です(笑)。
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。