【シフト演算①】シフト演算の考え方と論理シフトについて
2進数では、「シフト演算」という計算がよく行われます。10進数でもシフト演算を行うことはありますが、そんなに出番がありません。
しかし、2進数ではシフト演算を使うことで計算の効率がかなり上がるため、よく使われます。
今回は、そのシフト演算について解説していきます。
シフト演算とは
そもそもシフト演算ってどういうものなのかを定義します。
シフトという言葉は「位置を移動する」などの意味があります。シフト演算とは、その「シフト」を計算の過程で行うことです。つまり、数字を移動して計算を行うことをシフト演算といいます。
説明だけではよく分からないと思いますので、実際に一つ例を出してみましょう。
35を10倍する場合を考えるとします。このとき、皆さんはどのように計算を行うでしょうか?
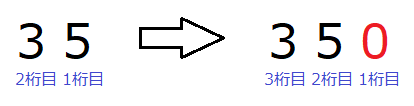
35+35+35+…というように、ずっと足していった人はいないと思います。多くの方が、35の数字全体を左にずらして0を一番下の桁に付け足しましたよね。このように、数字を移動させることで行う計算をシフト演算といいます。
2進数の例も考えてみましょう。「11(2進数)」を4倍するとき、どのように計算するのがいいでしょうか?
10進数の4は2進数では100です。こちらも、11+11+…と足していくこともできますが、シフト演算を使うともっと楽です。10進数では10倍で桁が1つ増えましたね。同じように考えると、2進数では2倍で桁が1つ増えることになります。今回は4倍にすることを考えます。2の2乗倍、つまり2桁増えることになります。下の桁に0を2つ増やせばいいので、1100が正解です。

この場合、1桁目と2桁目にあった「11」という数字2つを3桁目と4桁目に移しています。このように、上位桁の方向に数字をずらすことを、左シフトと呼びます。
シフト演算の定義が理解できたところで、論理シフトについて見ていきましょう。
論理シフト
論理シフトとは、符号を考慮せずにシフト演算を行う方法です。まず、先程と同じように、左シフトを行いましょう。00011010を2ビット分左にシフトする時を考えます。
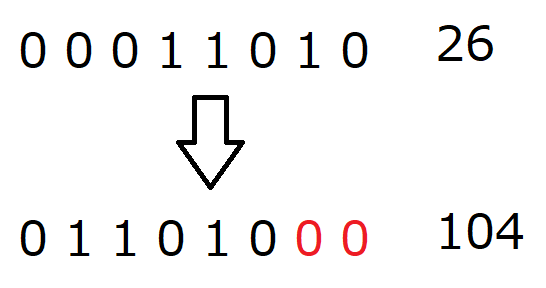
2ビット左にシフトすると、上の2桁がはみ出ますね。この溢れた2桁は削除します。そして、新たに空いた2桁は0で埋めます。そうすると、元の数字が10進数だと26であり、シフト後の数字は10進数表記で104なので、ちゃんと4倍になっていることが分かります。
では、右シフトはどのように行うのでしょうか。
手順は左シフトと同じです。数字を左にずらすのではなく右にずらすという違いがありますが、やることは同じです。では、1ビット右にシフトしてみましょう。理論上は、26の半分の13になります。
右にシフトし、溢れた数字は無視、新しく空いた桁には0を入れます。すると…
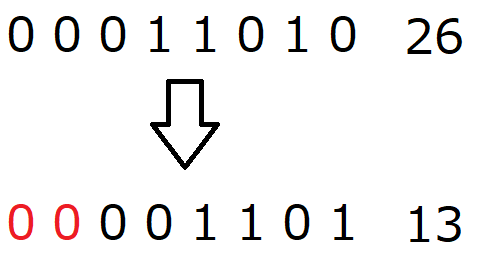
ちゃんと半分の13になっていますね。
注意点
今回は2ビット左シフトと1ビット右シフトを行いましたね。どちらも桁から溢れる数が0だったので無視しましたが、1が溢れた場合はどうなるでしょうか?
左シフトして104になりました。さらに2ビット左シフトすると、1が溢れますよね。この場合、1を無視すると、160になります。正しく4倍の計算が行われていません。このように、演算の結果がビット数で表せる範囲を超えてしまうことによって起きてしまうおかしな現象をオーバーフローと言います。
右シフトによって1が溢れた場合はどうでしょうか。00001101をさらに右に1ビットシフトすると、00000110となります。10進数表記では6ですね。ここではみ出た1は、割り算で言うところの余りに該当します。この場合は、オーバフローではありません。
まとめ
今回は、シフト演算の考え方と論理シフトについて解説しました。
数字全体を右や左方向に動かして、空いた桁に0を入れる操作を、シフト演算と言います。
論理シフトとは、シフト演算の中で符号を考慮しないシフト演算です。符号を考慮する算術シフトについては↓の記事で解説しています。
論理シフトの際、左シフトによって1が溢れた場合、オーバーフローが発生します。
というわけで今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。