【数学】なぜsin(90-θ)=cosθが成立するのか
今回は、ブログタイトルにもある通り、sin(90°-θ)=cosθとがどうして成立するのか？ということについて説明します。
また、cos(90°-θ)=sinθについても併せて説明します。ではtan(90°-θ)はどうなるんでしょうか？
その前に、sinとcosとtanについてよく分からないという方は以下の記事で解説しているので参考にしてみてください。
https://www.sumappu.com/post-143/結論
今回説明する式は以下の3つの式です。
\[\sin (90^\circ – \theta) = \cos \theta\]
\[\cos(90^\circ – \theta) = \sin \theta\]
\[\tan(90^\circ – \theta) = \frac{1}{\tan\theta}\]
今回はこの3つの式について解説していきます。
解説
sin(90-θ)について
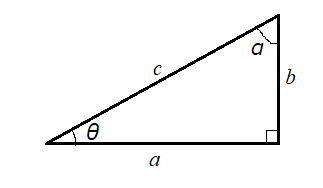
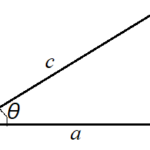
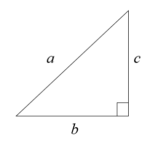
図1のような直角三角形について考えます。このとき、
\[\alpha = 90^\circ – \theta\]
が成り立つのは分かりますよね。三角形の内角の和は180度で、直角以外の2つの角度の和は90度ですから、当然ですよね。
では、sinαの値はどうなるでしょうか？
\[\sin \alpha = \frac{a}{c}\]
になりますよね。これって、cosθの値と同じになりますよね。
\[\sin \alpha = \sin (90^\circ – \theta) = \frac{a}{c} = \cos \theta \]であるから、
\[\sin (90^\circ – \theta) = \cos \theta \]
ですね。以上でsin(90°-θ)の証明は終わりです。
cos(90-θ)について
こちらも同様に考えると、
\[\cos (90^\circ – \theta) = \cos \alpha = \frac{b}{c} = \sin \theta \]であるから、
\[\cos (90^\circ – \theta) = \sin \theta \]ですね。
こちらも証明できました。
tan(90-θ)について
tan(90°-θ)の値を考えましょう。
\[\tan (90^\circ – \theta) = \tan \alpha = \frac{b}{a}\]
ですよね。tanθの値はどうかというと、b分のaです。
tanθとtan(90°-θ)の値って逆数の関係にありますよね。
なので、以下の式が成り立ちます。
\[\tan \theta \times \tan (90^\circ – \theta) = 1\]
両辺をtanθで割ることにより、
\[\tan (90^\circ – \theta) = \frac{1}{\tan \theta}\]
したがって、こちらも証明ができました。
まとめ
sinθ、cosθ、tanθについて、以下の式が成立します。
\[\sin (90^\circ – \theta) = \cos \theta\]
\[\cos (90^\circ – \theta) = \sin \theta\]
\[\tan (90^\circ – \theta) = \frac{1}{\tan \theta}\]
今回の内容は以上です。参考になったら嬉しいです。
他にも数学に関する投稿を上げていますので、気になるようなものがあれば覗いてみてください！
https://www.sumappu.com/category/math/最後までお読みいただき、ありがとうございました。