【物理に活かせる】三角形の斜辺から底辺と高さを求める
以前、sinとcosとtanについての解説をしました。
今回は、それらの知識を使って、斜辺の長さから三角形の高さと底辺の長さを算出する方法について考えます。
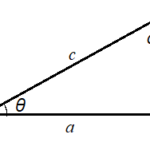
図1のような三角形があるとしましょう。
sinθとcosθとtanθは以下のように定義できます。
sinθ・cosθ・tanθの定義
\[ \sin \theta = \frac{b}{c} \] \[\cos \theta = \frac{a}{c} \] \[\tan \theta = \frac{b}{a} \]
上の式の導出過程は別の記事で説明しておりますので、そちらを参考にしてください。
式の変形
sinθとcosθとtanθについて定義できたところで、それぞれの定義の式を変形してみましょう。
\[ \sin \theta = \frac{b}{c} \] より \[b = c \sin \theta \]
このようになりますね。何も難しいことはしていません。左辺と右辺にcをかけただけです。
同様に、
\[ \cos \theta = \frac{a}{c} \] より \[a = c \cos \theta \]
のように式が変形できます。
tanθの式についても同様に式変形できますよね。他の2つと同じ流れなので、割愛します。
\[b = c \sin \theta \]と\[a = c \cos \theta \]から、次のことが分かります。
直角三角形において、
- 高さは、斜辺にsinθをかけることで得られる。
- 底辺は、斜辺にcosθをかけることで得られる。
三角形をグラフの中で書くと、高さはy軸方向に伸びて、底辺はx軸方向に伸びますよね。y軸方向は鉛直方向ともいうことがあります。x軸方向は水平方向と言ったりします。
ここまで理解できれば、次のような問も理解できると思います。
例題
問.傾斜30°の坂を50m登ったとき、鉛直方向に何m進んだか。(高さは何mか。)
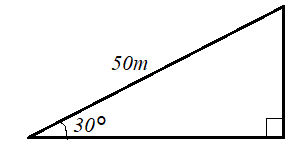
先程、鉛直方向の長さは斜辺の長さにsinθをかければ導出できると定義しましたので、
高さをyとすると、
\[ y = 50 \sin 30^\circ = 50 \times \frac{1}{2} = 25 \]
よって、鉛直方向には25m登ったことになります。
物理への応用
このsinθ、cosθ、tanθの応用的な考え方は、物理でよく使われます。
例えばハンドボール投げで、30°の方向に向かって1秒に5m進む速さで投げたときに、速さを水平方向と鉛直方向に分解して考えたりするわけです。
水平方向は一定の速さだけど、鉛直方向は重力の影響を受ける…とか、いろいろあります。
詳しくは、物理の記事で扱おうと思います。
ちなみにこの例は、力学という分野の中の斜方投射という単元で扱います。物理の中でかなり序盤に学習します。
まとめ

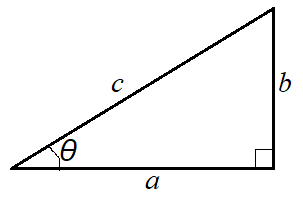
図3のような直角三角形において、斜辺をc、高さをb、底辺をaとすると、
\[ b = c \sin \theta\]
\[ a = c \cos \theta\]
また、\[ b = a \tan \theta\]
となります。
このことから、直角三角形の高さは斜辺の長さにsinθをかける、底辺の長さは斜辺の長さにcosθをかけることによって算出できます。
今回はここで終わりです。最後までお読みいただき、ありがとうございました。