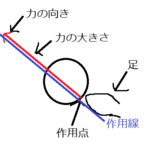
【力学】力のつり合いについて解説
今回は、「力のつり合い」について解説します。
今回の記事では、重力と張力が出てきます。
重力と張力については以前の記事で少し解説しています。
Contents
例題①
問題を使って解説していくことにします。
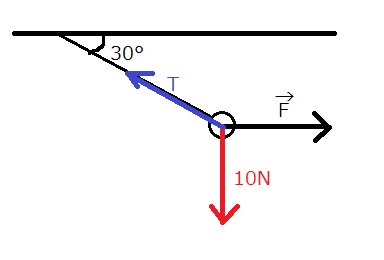
軽い糸に重さ(重力の大きさ)\(10N\)の小球をつけ、天井からつるす。
小球を水平方向に力\(\vec{F}\)で引き、糸が天井と\(30^\circ\)の角をなす状態で静止させた。
(1)糸が小球を引く力の大きさ\(T[N]\)を求めよ。
(2)力\(\vec{F}\)の大きさ\(F[N]\)を求めよ。

全ての力を書き出してみる
問題の図では、小球を水平方向に引っ張っている力\(\vec{F}\)についてのみ、図示されています。
しかし、他にも、球体の重力と、糸が引っ張る張力が関わってきています。
これら2つの力についても図示しないと、問題解決を進めることは困難です。
力の分解
ここで最初に考える必要があるのが、力の分解についてです。
力には合成・分解という考え方がありまして、
合成というのは、1つの物体に複数の力が同時に働く時に、同じ働きをする1つの力を求めることができるというものです。
合成された力のことを、合力といいます。
それとは逆の考え方が分解です。
1つの力を、いくつかの力に分けることを言います。
分けられた力のことを分力といいます。
鉛直方向と水平方向の力に分解
力の分解については理解していただけましたでしょうか?
物理にはお決まりのようなものがありますが、その中の一つに、
「複数の力が働いているときは水平方向と鉛直方向の力に分解して考える」
というものがあります。
今回の問題の場合、糸の張力\(T\)が水平方向(\(x\)軸方向)でも鉛直方向(\(y\)軸方向)でもない方向の力ですから、
水平方向と鉛直方向の力に分解してやります。
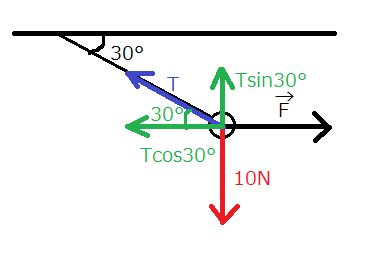
青色の矢印が張力\(T\)です。
それを水平方向と鉛直方向に分解したのが緑の矢印です。
\(\sin\)や\(\cos\)については過去の記事で解説しています。
「静止させた」という言葉の意味
静止しているということは、力が全く働いていないという意味にも取れますが、そのケースは物理ではあまりありません。
どちらかというと、複数の力がつり合っている状態です。
つり合っている状態というのは、つまり、合力が\(0\)になる状態のことを指しています。
分かりやすい例を出して説明します。
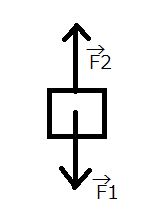
上図のように、重力\(\vec{F_1}\)と張力\(\vec{F_2}\)があって、この2つの力がつり合っているとき、
\(\vec{F_1}+\vec{F_2}=\vec{0}\)
という式が成立します。
水平方向と鉛直方向で力のつり合いを考える
問題を解くのに必要な知識・考え方の紹介が大体終わりましたので、問題の解説に入ります。
まず、鉛直方向の力のつり合いについて考えます。
上向きを正とすると、
\(T\sin 30^\circ+(-10)=0\)
つまり、\(T\sin 30^\circ=10\)ですね。
\(\sin 30^\circ=\frac{1}{2}\)ですから、
\(\frac{1}{2} \cdot T = 10\)
\(T=20\)
したがって、(1)の答えは\(T=20[N]\)です。
続いて、水平方向の力のつり合いを考えます。
右向きを正とすると、
\(\vec{F}+(-T\cos 30^\circ) = 0\)
\(\vec{F}=T\cos 30^\circ\)
\(T=20\)より、
\(\vec{F}=20\cdot \frac{\sqrt{3}}{2}\text{≒}17N\)
したがって、(2)の答えは\(F\text{≒}17[N]\)です。
例題②
例題①の解説、分かっていただけましたか?
もう1問解説して終わりにしたいと思います。
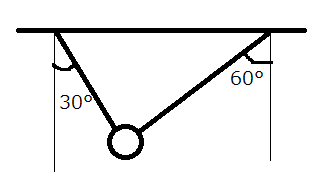
重さ(重力の大きさ)\(30N\)の小球に2本の軽い糸1、糸2をつけ、糸の他端を天井に固定して小球を正しさせた。
糸1、糸2が鉛直方向となす角をそれぞれ\(30^\circ\)、\(60^\circ\)とする。
糸1が引く力の大きさ\(T_1[N]\)と糸2が引く力の大きさ\(T_2[N]\)を求めよ。
解答(解説)
今回出てくる力は、糸の張力2つと重力ですね。
糸1の張力を\(T_1\)とし、糸2の張力を\(T_2\)とします。
鉛直方向について、\(T_1\)の鉛直成分の力と\(T_2\)の鉛直成分の力の合力が重力と等しくなっています。
水平方向について、\(T_1\)の水平成分の力と\(T_2\)の水平成分の力が等しいです。
したがって、以下のような連立方程式を立てることができます。
\[\begin{eqnarray} \left\{ \begin{array}{l}T_1 \cos 30^\circ + T_2 \cos 60^\circ = 30 \\ T_1 \sin 30^\circ = T_2 \sin 60^\circ \end{array} \right.\end{eqnarray}\]
鉛直方向は基本的に\(\sin\)を使うんですが、今回は\(\cos\)になります。
そこだけ注意です。
上の連立方程式を解くと…
\(T_1\text{≒}26[N]\)、\(T_2=15[N]\)となります。
というわけで、今回の内容はここまでです。何か参考になる情報があれば嬉しいです。
以下、少し余談です。
余談
今回の記事では、恐らく当ブログ史上初めて連立方程式を使ったのですが…
構文というかコマンドがめちゃくちゃ長い…(笑)
もう少し楽に入力できたらいいんですが、該当部分のコマンドがどうなっているか、興味ある方がいらっしゃるかどうか分かりませんが…
晒してみます。
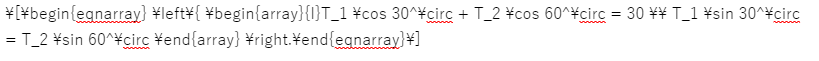
訳分からんでしょ…?笑
こんな長いコマンド、別の方のブログを参考にさせていただきましたので、そのリンクを貼りつけて今日は終わりにします。
今回は久しぶりの理系ネタでした。
最後までお読みいただき、ありがとうございました。