【三角比】センター試験(2014年度)の問題を解いてみる
2014年度の問題はコチラ↓で閲覧できます。
Contents
問題【前編】

解答(解説)【前編】
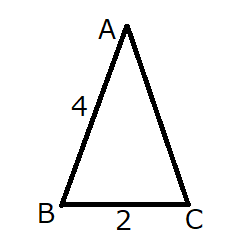
ア
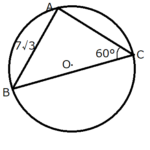
最初は\(CA\)を求める問題です。
余弦定理を使うことで求めることができます。
余弦定理の公式に値を当てはめて式を立てると…
\(AC^2=2^2+4^2-2\cdot 4 \cdot 2 \cdot \frac{1}{4}\)
これを解くと…
\[AC=4\]
イ・ウ
続いては\(\cos \angle BAC\)を求める問題です。

\(\cos \angle BAC\)も余弦定理を使って解くことができます。
公式に値を代入すると…
\(\cos \angle BAC = \frac{4^2+4^2-2^2}{2\cdot 4 \cdot 4}\)
これを解くと…
\[\cos \angle BAC = \frac{7}{8}\]
エ・オ・カ
続いて、\(\sin \angle BAC\)を求めます。
\(\sin^2 \angle BAC + \cos^2 \angle BAC = 1\)ですから、
\(\sin^2 \angle BAC = 1-\left(\frac{7}{8} \right)^2\)
\(\sin \angle BAC > 0\)より、
\[\sin \angle BAC = \frac{\sqrt{15}}{8}\]
キ・ク・ケ・コ・サ

次は、外接円の半径を求める問題です。
外接円の半径\(R\)は、次のようにして求められます。
\[2R = \frac{BC}{\sin \angle BAC}\]
各値を代入すると、次の式ができます。
\(2R=2 \cdot \frac{8}{\sqrt{15}}\)
これを解くと…
\[R=\frac{8\sqrt{15}}{15}\]
シ・ス

だんだんと図がややこしくなってきましたね…。
次は、\(AE\)の長さを求める問題です。
\(BE\)は、\(\angle ABC\)の二等分線です。したがって、\(AB:BC=AE:CE\)という関係が成立します。
\(4:2=AE:CE\)より、
\(AE=2CE \text{・・・(1)}\)
\(AC\)の長さは4ですから、\(AE+CE=4 \text{・・・(2)}\)
(1)式より、\(CE=\frac{1}{2}AE\)とすると、(2)式は以下のようになります。
\(AE+\frac{1}{2}AE=4\)
これを解くと…
\[AE=\frac{8}{3}\]
セ・ソ・タ・チ

続いては\(BE\)の長さを求める問題です。
\(\triangle ABE\)に着目して、余弦定理を使います。
ここで、\(\angle BAC = \angle BAE\)であることに気づきましょう。
公式に値を代入すると、次の式ができます。
\(BE^2 = 4^2+\left( \frac{3}{8} \right)^2 – 2\cdot 4 \cdot \frac{3}{8} \cdot \frac{7}{8}\)
これを解くと…
\[BE = \frac{2\sqrt{10}}{3}\]
ツ・テ・ト・ナ

三角形の3つの角の二等分線はすべて交わります。その交わった点のことを内心といいます。
ですから、\(D\)は内心です。\(\angle ACB\)の角の二等分線も考えると、
\(BC:CE=BD:DE\)という関係が成立します。
\(CE\)は\(AC-AE = \frac{4}{3}\)ですから、\(2:\frac{4}{3} = BD:DE\)より、\(DE=\frac{2}{3}BD\)
\(BE\)の長さはすでに求めていますから使いましょう。
\(BD+DE=BE\)より、\(BD+\frac{2}{3}BD=\frac{2\sqrt{10}}{3}\)
これを解くと…
\[BD=\frac{2\sqrt{10}}{5}\]
ニ・ヌ

次は、\(\triangle EBC\)と\(\triangle EAF\)の面積の関係を求める問題です。
上図の青で塗りつぶしている部分が\(\triangle EAF\)で、緑の部分が\(\triangle EBC\)です。
\(\angle AFE\)と\(\angle ECB\)はともに弧\(AB\)に対する円周角のため、角度の大きさが等しいです。
\(\angle EBC\)と\(\angle EAF\)はともに弧\(AB\)に対する円周角のため、角度の大きさが等しいです。
したがって、\(\triangle EBC\)と\(\triangle EAF\)は2つの角度の大きさが等しいため、相似であるといえます。
\(AE:EB=\frac{8}{3}:\frac{2\sqrt{10}}{3}\)ですから、\(\triangle EAF\)と\(\triangle EBC\)の相似比は\(4:\sqrt{10}\)です。
面積比は相似比の2乗ですから、面積比は\(16:10\)つまり\(8:5\)です。
\(\triangle EAF : \triangle EBC=8:5 \)より、
\(\triangle EBC\)の面積は、\(\triangle EAF\)の面積の\(\frac{5}{8}\)倍
問題【後編】

解答(解説)【後編】
ネ
まず、\(FA\)の長さについて考えてみます。
\(FA:BC=4:\sqrt{10}\)より、\(FA=\frac{4\sqrt{10}}{5}\)となります。
続いて、\(FC\)についてです。
\(\triangle EAB\)と\(\triangle EFC\)が相似の関係になることを利用します。
\(BE=\frac{2\sqrt{10}}{3}\)、\(CE=\frac{4}{3}\)より、 \(\triangle EAB\)と\(\triangle EFC\) の相似比は…\(\sqrt{10}:2\)です。
したがって、\(AB:FC=\sqrt{10}:2\)より、\(FC=\frac{4\sqrt{10}}{5}\)となります。
この時点で、\(FA=FC\)ですから、選択肢①④⑥のいずれかとなります。
最後に\(FD\)を考えます。
\(FD=FE+ED\)という風に分解して考えていきます。
\(DE\)について
\(BD:DE=2:\frac{4}{3}\)でした。\(BD=\frac{2\sqrt{10}}{5}\)ですから、\(DE=\frac{4\sqrt{10}}{15}\)です。
\(FE\)について
\(FE:EC=4:\sqrt{10}\)より、\(FE:\frac{4}{3}=4:\sqrt{10}\)
これを解くと、\(FE=\frac{8\sqrt{10}}{15}\)
最後に、\(DE+FE=FD\)ですから…
\(FD=\frac{4\sqrt{10}}{15}+ \frac{8\sqrt{10}}{15} =\frac{4\sqrt{10}}{5}\)
したがって、④が正解となります。
まとめ
2014年度の三角比の問題を解くために必要な知識は…
- 余弦定理
- 外接円の半径の求め方
- 円周角の定理
- 三角形の相似について
といったところでしょうか。
三角比以外にも、相似や円周角といった中学数学の知識も必要になってくるので、数学が積み重ねの学問であることを身に染みて感じます。
ということで、今回の記事はここまでです。何か参考になる情報があれば嬉しいです。
ちなみに、他にもこのブログでは高校数学の解説を行っているので、ぜひ参考にしてみてください。
最後までお読みいただき、ありがとうございました。