【三角比】センター試験の問題を解いてみる(2015年度)
2015年度のセンター試験の問題はコチラ↓で閲覧できます。
問題
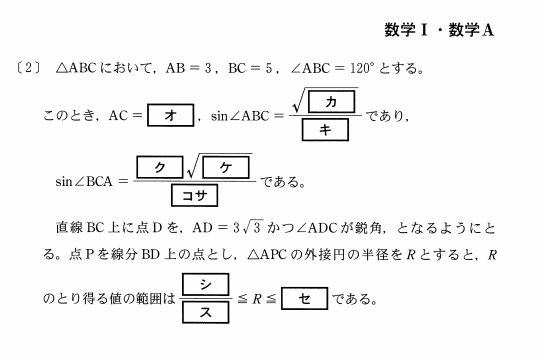
解答(解説)
オ

\(AC\)の長さを求める問題です。余弦定理を使います。
\[AC^2=AB^2+BC^2-2AB\cdot BC \cdot \cos \angle ABC\]
余弦定理の公式に各値を代入すると…
\(AC^2=3^2+5^2-2\cdot 3 \cdot 5 \cdot \left( -\frac{1}{2} \right)\)
これを解くと…
\[AC = 7\]
カ・キ
\(\sin \angle ABC\)を求める問題です。
問題文の中に\(\angle ABC = 120^\circ\)とありますから…
\[\sin \angle ABC = \frac{\sqrt{3}}{2}\]
ク・ケ・コ・サ
\(\sin \angle BCA\)を求める問題です。
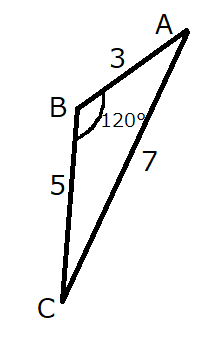
余弦定理を変形してから使います。
\[\cos \angle BCA = \frac{AC^2+BC^2-AB^2}{2AC \cdot BC}\]
上の式に各値を代入します。
\(\cos \angle BCA = \frac{5^2+7^2-3^2}{2\cdot 5 \cdot 7}\)
これを解くと…
\(\cos \angle BCA = \frac{13}{14}\)
\(\sin^2 \theta + \cos^2 \theta = 1\)より、
\(\sin^2 \angle BCA + \left(\frac{13}{14} \right)^2 = 1\)
\(\sin^2 \angle BCA = \frac{27}{196}\)
\(\sin \angle BCA = \pm \frac{3\sqrt{3}}{14}\)
\(\sin \angle BCA > 0\)より、
\[\sin \angle BCA = \frac{3\sqrt{3}}{14}\]
シ・ス・セ
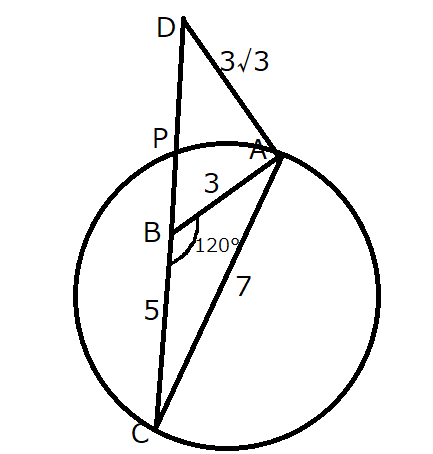
最後の問題は、\(\triangle APC\)の外接円の半径\(R\)の取り得る範囲ですね。
点\(P\)は\(BD\)上を動きます。
半径\(R\)が最小になるときと最大になるときが、どのようなときなのかを考える必要があります。
まずは、半径が最大になるときについて考えます。
半径が最大になるとき
これは、点\(P\)が\(D\)と重なっているときです。
\(\angle BCA = \angle ACD\)ですから、\(\sin ACD = \frac{3\sqrt{3}}{14}\)
外接円の半径\(R\)は次の公式で求めることができます。
\[2R = \frac{AD}{\sin \angle ACD}\]
上の公式に各値を代入すると…
\(2R=\frac{3\sqrt{3}}{14}\)
これを解くと、
\[R=7\]
半径が最小になるとき
外接円の半径が最小になるときはどのようなときかと言いますと…
\(AP\)の長さが最も短いときです。実はこのとき、\(\angle APC=90^\circ\)となります。
つまり、\(\angle APC\)が直角です。
円周角の定理より、\(AC\)が外接円の直径の長さと等しいですから、外接円の半径\(R\)は\(AC\)の半分です。
つまり…
\[R=\frac{7}{2}\]
以上より、外接円\(R\)の範囲は
\[\frac{7}{2} \text{≦} R \text{≦}7\]
まとめ
2015年度の問題で必要な知識は…
- 余弦定理
- 三角形の外接円の半径の求め方
- 円周角の定理
といったところでしょうか。
今回の記事の内容は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。