【力学】水平投射とは？

2021年7月5日

物体をある高さから水平方向に投げ出すと、物体は放物線を描いて飛んでいきます。その後、地面に達します。

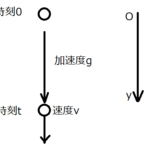
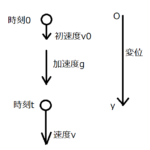
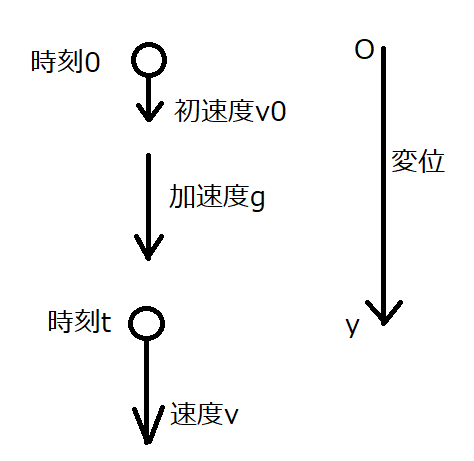
この運動を、水平投射と言います。図にすると、こんな感じです↓

めちゃくちゃ雑な絵ですみません…。ただ、「ある高さから物体を水平方向に投げると、自然に落ちていくよね」っていうのが頭で想像できれば、それでOKです！

では、水平投射の概要を理解したところで、この水平投射について、掘り下げていきます。

水平投射とは

今まで、自由落下や鉛直投げ下ろし・鉛直投げ上げといった、落体の運動を扱ってきました。

これまでの落体の運動と水平投射では大きな違いが1つあります。

それは…

水平投射は水平方向にも運動しているということです。

自由落下などは鉛直方向にしか運動していませんが、水平投射は鉛直方向＋水平方向の異なる2つの方向に運動しています。

では、鉛直方向と水平方向に分解して考えていきます。

鉛直方向

鉛直方向っていうのは、重力が働く方向ですね。

水平投射では、鉛直方向には自由落下と同様の運動をしています。

水平方向には初速を加えていますが、鉛直方向には力を加えていません。重力の影響だけを受けて下に静かに落ちていきます。

水平方向

水平方向は、鉛直方向と直交する方向のことです。つまり、鉛直方向と垂直な方向が水平方向です。

水平投射では、水平方向には等速直線運動と同様の運動をしています。等速直線運動についてはコチラ↓

重力のような外部からの力がないため、速さは投げ出したときと同じ速さがずっと維持されます。

水平投射の公式

水平投射は\(x\)軸方向（水平方向）と\(y\)軸方向（鉛直方向）に分けて公式を導出していきます。

\(x\)軸方向については等速直線運動と同様の運動をするんでしたね。ですから、等速直線運動の公式（\(x=vt\)）より、

• \(v_x=v_0 \text{ ・・・(25)}\)
• \(x=v_0t \text{ ・・・(26)}\)

\(v_x\)は\(x\)軸方向の速度を表しています。

(25)式は、水平投射の\(x\)軸方向の速度は初速から変わらないことを意味しています。

(26)式は、\(x=v_xt\)とすることも可能です。

続いて、\(y\)軸方向の運動について考えます。\(y\)軸方向は自由落下と同様の運動をしますから、自由落下の公式より、

• \(v_y=gt \text{ ・・・(27)}\)
• \(y=\frac{1}{2}gt^2 \text{ ・・・(28)}\)
• \(v_y^2=2gy \text{ ・・・(29)}\)

という3つの式を導出できます。

(27)式は自由落下の公式\(v=gt\)、(28)式は\(y=\frac{1}{2}gt^2\)、(29)式は\(v^2=2gy\)を使っています。

\(v\)が\(v_y\)に変わっているだけです。

ちなみに、(26)式と(28)式から\(t\)を消去すると、

\[y=\frac{g}{2v_0^2}\cdot x^2\]

という式になります。この式を見て何か気づきませんか…？

式の最後に\(x^2\)とあります。つまり、2次関数です。

したがって、水平投射の運動の軌道は、原点を頂点とし、\(y\)軸を軸とした2次関数の概形を描くということができます。

例題

まとめ

今回の記事のまとめです。

ということで、今回の記事はここまでです。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。