【三角比】センター試験の問題を解いてみる（2017年度）

2021年7月3日

2017年度の問題はコチラで閲覧可能です↓

問題

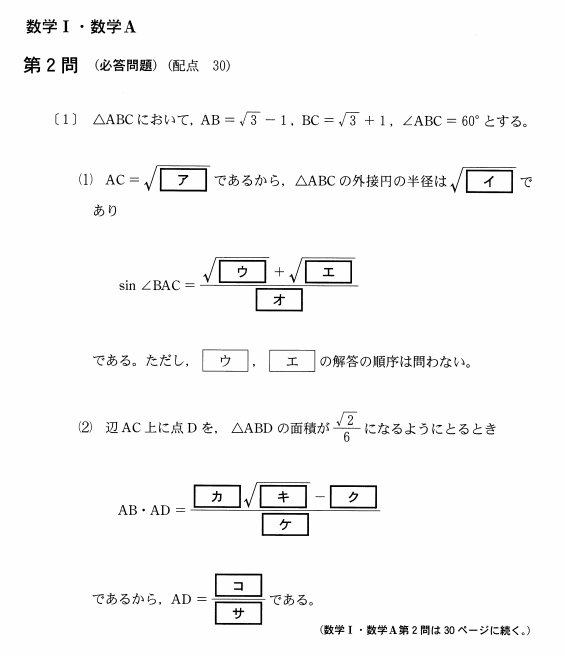
解答（解説）

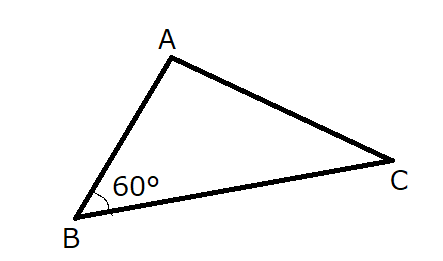
ア

\(AB=\sqrt{3}-1\)、\(BC=\sqrt{3}+1\)、\(\angle ABC=60^\circ\)が現時点で分かっていることです。

余弦定理を使うことで、\(AC\)の長さも分かります。

\(AC^2=(\sqrt{3}-1)^2+(\sqrt{3}+1)^2-2\cdot (\sqrt{3}-1)\cdot (\sqrt{3}+1)\cdot \frac{1}{2}\)

これを解くと、

\[AC=\sqrt{6}\]

イ

正弦定理より、

\(2R=\sqrt{6} \cdot \frac{2}{\sqrt{3}}\)

これを解くと、

\[R=\sqrt{2}\]

ウ・エ・オ

ここでも余弦定理の登場です。

\(AB=\sqrt{3}-1\)、\(BC=\sqrt{3}+1\)、\(AC=\sqrt{6}\)より、

\(\cos \angle BAC = \frac{(\sqrt{3}-1)^2+(\sqrt{6})^2-(\sqrt{3}+1)^2}{2 \cdot (\sqrt{3}-1)\cdot \sqrt{6}}\)

これを解くと、

\(\cos \angle BAC = \frac{\sqrt{2}-\sqrt{6}}{4}\)

\(\sin^2 \theta + \cos^2 \theta = 1\)より、

\(\sin \angle BAC = \sqrt{1-\left(\frac{\sqrt{2}-\sqrt{6}}{4} \right)^2}\)

これを解くと、

\[\sin \angle BAC = \frac{\sqrt{6}+\sqrt{2}}{4}\]

カ・キ・ク・ケ

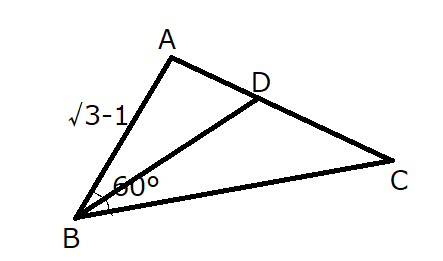
面積を求める公式に、\(S=\frac{1}{2} bc \sin A\)というものがあります。それを使います。

\(S=\frac{1}{2}\cdot AB \cdot AD \sin \angle BAD\)

\(\sin \angle BAD\)は、\(\sin \angle BAC\)と同じです。また、\(S=\frac{\sqrt{2}}{6}\)となりますから、

\(\frac{\sqrt{2}}{6}=\frac{1}{2}\cdot AB \cdot AD \cdot \frac{\sqrt{6}+\sqrt{2}}{4}\)

これを解くと、

\[AB \cdot AD = \frac{2\sqrt{3}-2}{3}\]

コ・サ

先程、\(AB \cdot AD = \frac{2\sqrt{3}-2}{3}\)を導出しました。

ここに、既に値が分かっている、\(AB=\sqrt{3}-1\)を代入します。

すると、\((\sqrt{3}-1)\cdot AD = \frac{2\sqrt{3}-2}{3}\)

式変形すると、\(AD\)の答えが出てきます。

\[AD=\frac{2}{3}\]

まとめ

2017年度の三角比の問題を解く上で必要な知識は…

といったところですかね。

というわけで、今回の記事は以上です。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。