【三角比】センター試験の問題を解いてみる(2018年度)
2018年度の問題はコチラで閲覧できます↓
問題【前編】
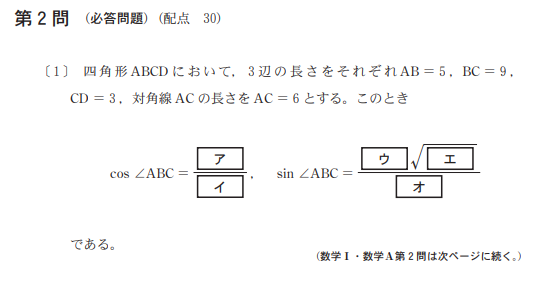
解答(解説)【前編】
ア・イ
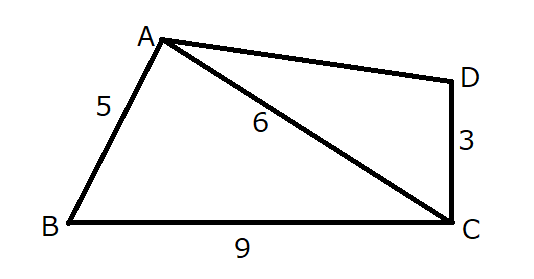
余弦定理を使います。
\(\cos \angle ABC = \frac{5^2+9^2-6^2}{2\cdot 5\cdot 9} = \frac{7}{9}\)
したがって、
\[\cos \angle ABC = \frac{7}{9}\]
ウ・エ・オ
\(\sin^2 \theta + \cos^2 \theta = 1\)より、
\(\sin^2 \angle ABC = \frac{32}{81}\)
\(0^\circ <\angle ABC < 180^\circ\)より、\(\sin \angle ABC > 0\)ですから、
\[\sin \angle ABC = \frac{4\sqrt{2}}{9}\]
問題【後編】
解答(解説)【後編】
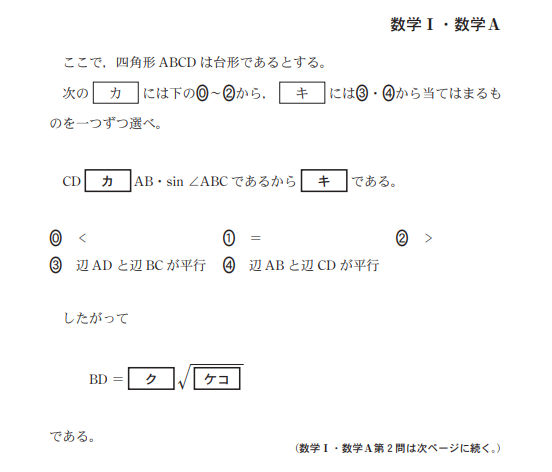
カ
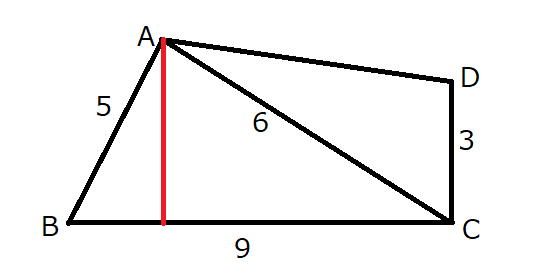
\(AB\cdot \sin \angle ABC\)は、赤線部分の長さですね。
\(AB\cdot \sin \angle ABC = 5\cdot \frac{4\sqrt{2}}{9}\)
ここで、\(\sqrt{2}=1.4\)とすると、\(AB\cdot \sin \angle ABC = 3.111111…\)です。
したがって、
\[CD < AB\cdot \sin \angle ABC \]
キ
\(CD < AB\cdot \sin \angle ABC \)が成り立つということが分かりましたね。
この時点で、\(AB\)と\(CD\)が平行であることは絶対にあり得ないのです。
なぜかと言いますと、、、
\(AB\cdot \sin \angle ABC \)は、\(A\)と\(CD\)の間を結ぶ最短距離なんです。もし、\(AB\)と\(CD\)が平行であるならば、\(CD\text{≧}AB\cdot \sin \angle ABC\)となっていなければならないのです。
これは、これ以上分かりやすく説明するのが難しいです…。実際に自分で図を描いたり頭の中で図を思い浮かべながら閃いてもらうしかないです…。
ク・ケ・コ
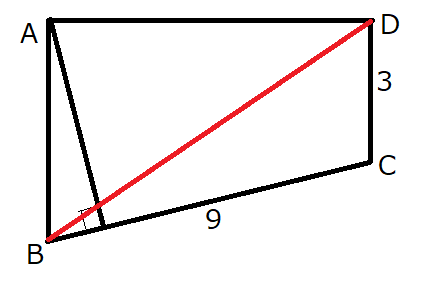
余弦定理を使って\(BD\)を求めたいですが、\(\angle BCD\)の角度の情報がないので、このままでは不可能です。
ここで、ある台形の性質を使います。
それは、、、
同側の内角の和は\(180^\circ\) つまり \(\angle ABC + \angle BCD = 180^\circ\)ということです。
したがって、\(\cos(180^\circ – \angle ABC) = \cos \angle BCD\)となるわけです。
\(\cos(180^\circ – \angle ABC) = -\frac{7}{9}\)ですから、\(\cos \angle BCD = \frac{7}{9}\)です。
では、最後に、余弦定理を使ってやることによって、
\(BD^2=9^2+3^2-2\cdot 9\cdot 3\cdot \left(-\frac{7}{9} \right)\)
計算すると、
\[BD = 2\sqrt{33}\]
まとめ
今回の問題を解く上で必要な知識のまとめです。
- 余弦定理
- \(\sin^2 \theta + \cos^2 \theta = 1\)
- 台形の同側の内角の和は\(180^\circ\)
- \(\cos(180^\circ – \theta) = -\cos \theta\)
台形の同側の内角の和が180°というのは、ネットで調べてたどり着いたのですが、教科書とかで習った経験はないような…?
ということで、今回の記事の内容は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。