【三角比】センター試験の問題を解いてみる(2019年度追試)
2019年度の追試問題が紹介されているセンター試験サイトのリンクはコチラ↓
問題【前編】

解答(解説)【前編】
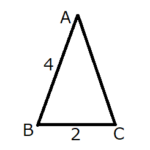
ア・イ

赤で描いた部分は、問題文で記載されていませんが、解答をするにあたって分かりやすくなるので追記しました。
\(AB \cdot \cos \angle ABC + AC \cdot \cos \angle ACB = BE + EC\)です。
なぜ、この式が成り立つかというと、\(\triangle ABE\)について\(BE = AB \cdot \cos \angle ABC\)となるわけです。同様に、\(CE = AC \cdot \cos \angle ACB\)です。
\(BE + EC = BC\)ですから、ア・イの答えは 12 です。
ウ・エ
正弦定理より、\(\frac{AB}{\sin \angle ACB} = \frac{AC}{\sin \angle ABC}\)の関係が成り立ちます。これを変形すると、
\(\frac{AB}{AC} = \frac{\sin \angle ACB}{\sin \angle ABC}\)となります。
\(\sin \angle ABC\)は、\(\sin^2 \angle ABC + \cos^2 \angle ACB = 1\)より、\(\frac{2\sqrt{2}}{3}\)
\(\sin \angle ACB\)は、\(\frac{4\sqrt{2}}{9}\)です。
\(\frac{\sin \angle ACB}{\sin \angle ABC} =\frac{4\sqrt{2}}{9} \times \frac{3}{2\sqrt{2}} = \frac{2}{3}\)
したがって、
\[\frac{AB}{AC} = \frac{2}{3}\]
問題【後編】

解答(解説)【後編】
オ カ・キ
\(\frac{AB}{AC} = \frac{2}{3}\)より、\(AB = \frac{2}{3} AC\)
\(AB = \frac{2}{3} AC\)を、\(AB \cdot \cos \angle ABC + AC \cdot \cos \angle ACB = 12\)に代入します。さらに、\(\cos \angle ABC = \frac{1}{3}\)、\(\cos \angle ACB = \frac{7}{9}\)も代入して、式を整理すると、
\[AC = 12\]
\(AB = \frac{2}{3} AC\)より、
\[AB = 8\]
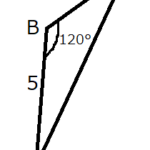
ク・ケ・コ

余弦定理より、
\(AD^2 = 8^2+6^2 -2\cdot 8 \cdot 6 \cdot \frac{1}{3}\)
これを解くと、\[AD = 2\sqrt{17}\]
ちなみに、\(AD^2=AC^2+CD^2-2AC \cdot CD \cdot \cos \angle ACB\)と考えても同じ答えが出てくるはずです。
まとめ
今回のこの問題を解く上で必要な知識は…
- 正弦定理
- 余弦定理
- \(\sin^2 \theta + \cos^2 \theta = 1\)
私自身が解いて思ったのは、一番最初のア・イが一番難しかったです。難しいというより、閃きに時間がかかったといったほうが正しいでしょうか。
ということで、この記事の内容は以上です。
何か参考になれば嬉しいです。
最後までお読みいただき、ありがとうございました。