【2次関数】センター試験の問題を解いてみる(2001年度)
2001年度の問題のリンクはコチラ↓
問題
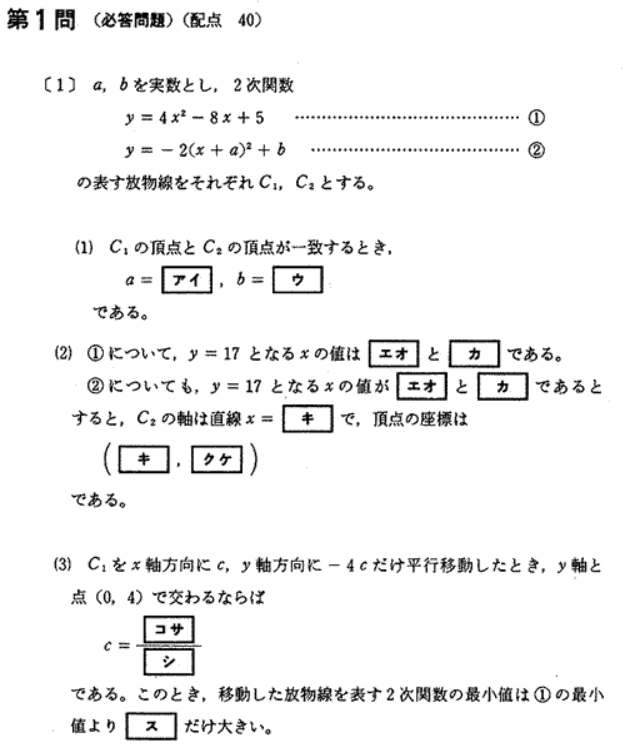
解答(解説)
ア・イ・ウ
①のグラフの式を平方完成すると、\(y=4(x-1)^2+1\)
したがって、頂点は点\((1,1)\)
②のグラフの頂点は、点\((-a,b)\)
以上から、①と②のグラフの頂点が一致する時は、
\[a=-1\]
\[b=1\]
エ・オ・カ
\(4x^2-8x+5=17\)より、
\[x=-1,3\]
キ・ク・ケ
②についても、\(x=-1\)と\(x=3\)のときに\(y=17\)になると書いてあるので、
\(-2(-1+1)^2+b=17\)
\(-2(3+a)^2+b=17\)
という2つの式が立ちます。
この2つの式を解くと、\(a=-1,b=25\)
この\(a\)と\(b\)の値を②に代入すると…
\(y=-2(x-1)^2+25\)
したがって、頂点の座標は、
点\((1,25)\)となります。
コ・サ・シ
\(C_1\)を\(x\)軸方向に\(c\)、\(y\)軸方向に\(-4c\)だけ平行移動すると、頂点は\((1+c,1-4c)\)です。
したがって、グラフの式は\(y=4\{x-(1+c)\}^2+1-4c\)
これに\(x=0,y=4\)を代入すると、\(4=4(-c-1)^2+1-4c\)
これを解くと、\[c=-\frac{1}{2}\]
ス
\(y=4\{x-(1+c)\}^2+1-4c\)に\(c=-\frac{1}{2}\)を代入すると、
\(y=4\left(x-\frac{1}{2}\right)^2+3\)
頂点(最小値)は\((\frac{1}{2},3)\)となります。本来の頂点(最小値)は\((1,1)\)でしたから、最小値は2だけ大きくなっています。
まとめ
今回の問題を解いていく中で、少しコツというかテクニックが必要だと感じた箇所がありますので、その部分を少しだけまとめておきます。
\(y=(x-a)^2\)のグラフを\(x\)軸方向に3、\(y\)軸方向に4だけ平行移動させると、\(y=\{x-(a+3)\}^2+4\)というグラフになる。
というわけで、今回の内容は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。


