【2次関数】センター試験の問題を解いてみる(2003年度)
2003年度の問題のリンクはコチラ↓
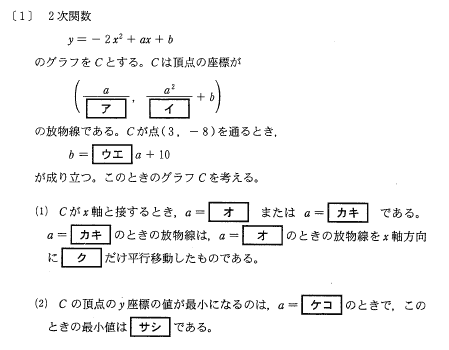
問題
解答(解説)
ア・イ
放物線\(C\)の式\(y=-2x^2+ax+b\)を平方完成します。すると、
\(y=-2\left(x-\frac{a}{4}\right)^2+\frac{a^2}{8}+b\)
したがって、頂点は
\[\left(\frac{a}{4},\frac{a^2}{8}+b\right)\]
ウ・エ
\(C\)の式に\(x=3,y=-8\)を代入します。
\(-8=-18+3a+b\)より、
\[b=-3a+10\]
オ カ・キ
グラフが\(x\)軸と接するとき と来たら、 判別式\(D=0\)です。
\(D=b^2-4ac\)より、
\(a^2-4\cdot(-2)\cdot(-3a+10)=0\)
これを解くと、
\[a=4,20\]
ク
\(a=20\)のときのグラフの式は\(y=-2x^2+20x-50\)です。これを平方完成すると、\(y=-2(x-5)^2\)
したがって、頂点は\((5,0)\)です。
\(a=4\)のときのグラフの式は\(y=-2x^2+4x-2\)です。こちらの頂点は\((1,0)\)です。
以上より、\(a=4\)の時の放物線を\(x\)軸方向に1だけ平行移動すると\(a=20\)のときと同じものになります。
ケ・コ サ・シ
頂点の\(y\)座標は、\(\frac{a^2}{8}+b\)でした。
ウ・エより、\(b=-3a+10\)ですから、\(\frac{a^2}{8}-3a+10\)となります。これを\(Y\)とします。
\(Y=\frac{a^2}{8}-3a+10\)
平方完成すると、\(Y=\frac{1}{8}(a-12)^2-8\)
したがって、\(C\)の頂点の\(y\)座標は、\(a=12\)のときに最小値\(-8\)をとります。
まとめ
今回のポイントのまとめです。
- グラフと\(x\)軸が接するための条件:判別式\(D=0\)
- \(D=b^2-4ac\)
- グラフの頂点の\(y\)座標の最小値を求めるとき:\(y\)座標を1つの関数として扱い、平方完成などを経ることによって最小値を得ることができる
ということで、今回の内容は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。