【力学】速度③(速度の合成・分解)
等速直線運動などについてはコチラ↓
変位や、平均・瞬間の速度についてはコチラ↓
速度の合成
直線上の速度の合成
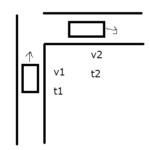
風の強い道を車が8m/sで走っているとします。このとき、風が2m/sで車の進行方向とは逆方向に吹いていたとしましょう。わざわざ描くほどでもないとは思いますが、図にすると、↓のような状態です。
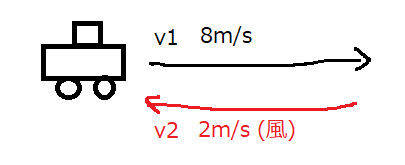
車の進行方向を正とします。車の速度を\(v_1\)、風の速度を\(v_2\)とすると、\(v_1=8m/s\)、\(v_2=-2m/s\)となり、見かけ上の速度は\(6m/s\)になります。この見かけ上の速度を合成速度といい、合成速度を求めることを速度の合成といいます。
では、風が逆向きに吹いているとどうでしょうか。つまり向かい風ではなく追い風になります。そのときは\(v_1=8m/s\)、\(v_2=2m/s\)ですから、合成速度は\(10m/s\)になります。
以上より、合成速度は以下の式で求めることができます。
\[v=v_1+v_2\text{・・・(4)}\]
平面上の速度の合成
では、次は川を横切る船について考えてみましょう。船の速度を\(\vec{v_1}\)、川を流れる水の速度を\(\vec{v_2}\)とします。
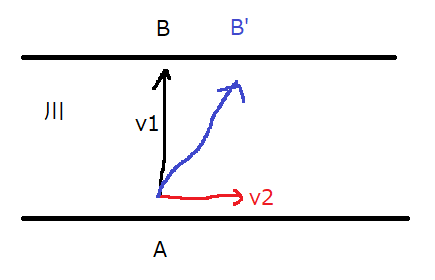
Aにいた船がBに向けて出発しますが、川を流れる水の影響でB’の方向に向かってしまいます。よって、川岸から見た船の速度\(\vec{v}\)の大きさは次のように表されます。
\[\vec{v}=\vec{v_1}+\vec{v_2}\text{・・・(5)}\]
流水の長さが\(3.0m/s\)のまっすぐな川を、船が川岸に対して垂直な方向へ船首を向けて出発する。静水時の船の速さを\(4.0m/s\)とするとき、川岸から見た船の速さ(速度の大きさ)は何\(m/s\)か。
\(v=\sqrt{3.0^2+4.0^2}=5.0\)
\(5.0m/s\)
速度の分解
(5)式は2つの速度\(\vec{v_1}\)と\(\vec{v_2}\)を足して速度を合成するというものでした。ということは、1つの速度\(\vec{v}\)を2つの速度\(\vec{v_1}\)と\(\vec{v_2}\)に分解できると考えることもできます。このような場合、速度を分解できるといえます。分解した2つの速度を分速度といいます。分解速度とは呼ばないようなので注意しましょう。
速度の成分
速度の分解は、\(x\)軸方向と\(y\)軸方向に分解することがほとんどです。このとき、分速度\(\vec{v_x}\)、\(\vec{v_y}\)の大きさに正・負の符号(向きを表す)をつけた値\(v_x\)、\(v_y\)を、速度\(\vec{v}\)の\(x\)成分、\(y\)成分と言います。
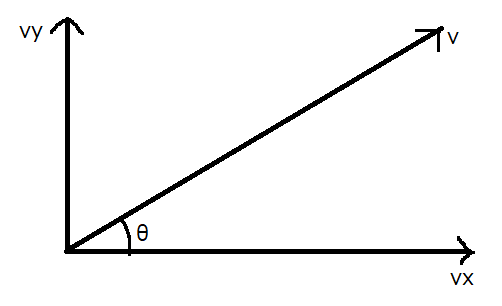
速度\(\vec{v}\)が\(\vec{v_x}\)となす角を\(\theta\)、\(\vec{v}\)の\(x\)成分を\(v_x\)、\(\vec{v}\)の\(y\)成分を\(v_y\)とするとき、これらの間には次の関係が成り立ちます。
\[v_x=v\cos\theta, v_y=v\sin\theta\text{・・・(6)}\]
\[v=\sqrt{v_x^2+v_y^2}\text{・・・(7)}\]
また、2つの速度\(\vec{v_1}\)(\(x\)成分\(v_{1x}\)、\(y\)成分\(v_{1y}\))、\(\vec{v_2}\)(\(x\)成分\(v_{2x}\)、\(y\)成分\(v_{2y}\))の合成速度\(\vec{v}\)の\(v_x\)と\(v_y\)は各成分の和で求められます。
\[v_x=v_{1x}+v_{2x},v_y=v_{1y}+v_{2y}\text{・・・(8)}\]
水の流れがない水路を、船が岸となす角\(60^\circ\)の向きに速さ\(3.0m/s\)で進む。このとき、船の速度の\(x\)成分\(v_x\)[\(m/s\)]、\(v_y\)[\(m/s\)]を求めよ。
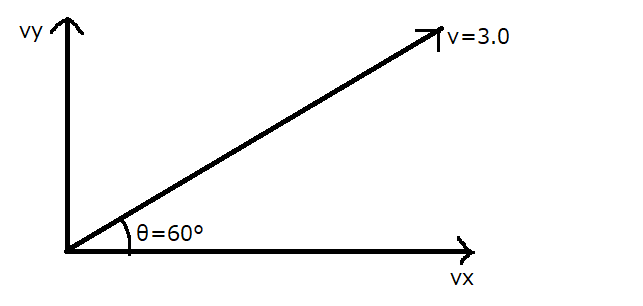
\(v_x=3.0\sin60^\circ=3.0\times\frac{1}{2}=1.5\)
\(v_y=3.0\cos60^\circ=3.0\times\frac{\sqrt{3}}{2}\text{≒}2.565\)
\(v_x=1.5m/s\)
\(v_y=2.6m/s\)
まとめ
- 2つの速度を足すことを速度の合成という。速度の合成によって得られた速度を合成速度という。
- 1つの速度を2つの速度に分解することを速度の分解という。速度の分解によって得られた速度を分速度という。
速度の合成・分解から三角関数の知識が必要になってきます。ですので、物理を勉強するうえで数学の勉強は必須ですね。
ということで、今回の内容はここまでです。何か参考になる情報があれば嬉しいです。
最後までお読みいただきありがとうございました。