【2次関数】センター試験の問題を解いてみる（2005年度）

2021年5月9日

今回扱う問題のリンクはコチラ↓

問題【前編】

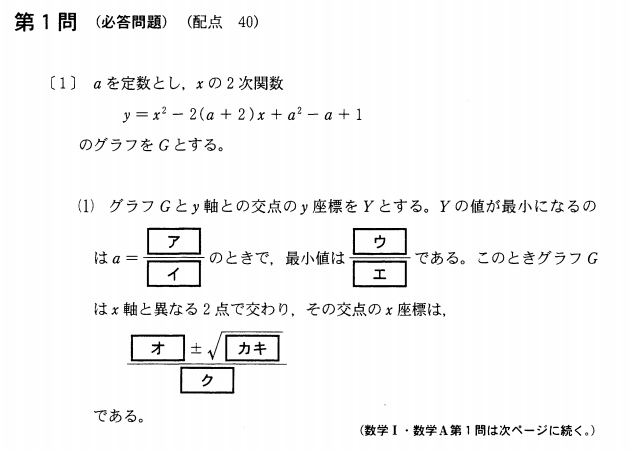
解答（解説）【前編】

ア・イ・ウ・エ

グラフと\(y\)軸の交点の\(y\)座標は、グラフの式に\(x=0\)を代入することによって求めることができます。

\(y=x^2-2(a+2)x+a^2-a+1\)に\(x=0\)を代入すると、\(a^2-a+1\)

\(a^2-a+1\)を平方完成すると、\(a-\frac{1}{2})^2+\frac{3}{4}\)

したがって、\(a=\frac{1}{2}\)のときに最小値\(\frac{3}{4}\)をとります。

オ・カ・キ・ク

\(x\)軸と交わるときの\(x\)座標は、\(y=0\)を代入することによって求めることができます。

\(y=x^2-2(a+2)x+a^2-a+1\)に\(y=0\)を代入すると、\(x^2-2(a+2)x+a^2-a+1=0\)

さらに、アイウエで求めた\(a=\frac{1}{2}\)を代入すると、\(x^2-5x+\frac{3}{4}=0\)

これを解くと、\(x\)座標が得られます。その座標は、

\[x=\frac{5\pm\sqrt{22}}{2}\]

問題【後編】

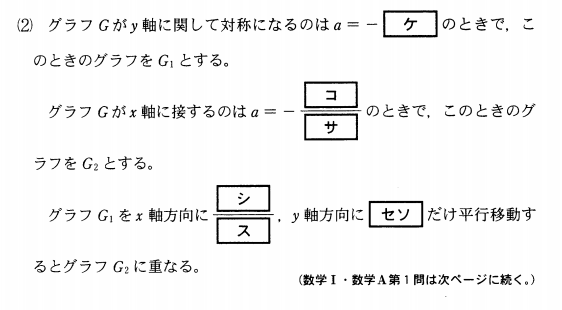
解答（解説）【後編】

ケ

\(y\)軸に関して対称ということは、頂点の\(x\)座標が0であるということです。

\(y=x^2-2(a+2)x+a^2-a+1\)を平方完成すると、\(y=\{x-(a+2)\}^2-5a-3\)

頂点の\(x\)座標は\(a+2\)です。

\(a+2=0\)より

\[a=-2\]

コ・サ

\(x\)軸に接するということは、判別式\(D=0\)です。\(D=b^2-4ac\)より、

\(\{2(a+2)\}^2-4(a^2-a+1)=0\)

これを解くと、

\[a=-\frac{3}{5}\]

シ・ス・セ・ソ

\(a=-2\)のときが\(G_1\)で、\(a=-\frac{3}{5}\)のときが\(G_2\)です。\(G\)の式\(y=x^2-2(a+2)x+a^2-a+1\)にそれぞれ代入すると、

\(G_1\text{:}y=x^2+7\)

\(G_2\text{:}y=(x-\frac{7}{5})^2\)

したがって、\(G_1\)を\(x\)軸方向に\(\frac{7}{5}\)、\(y\)軸方向に\(-7\)だけ平行移動すると、\(G_2\)に重なります。

まとめ

今回の問題を解く上でのポイントを下記にまとめてみました。

今回はここで終わりです。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。