【2次関数】センター試験の問題を解いてみる（2012年）

2021年5月3日

問題【前編】

解説【前編】

ア　イ　ウ

\(y=-x^2+(2a+4)x+b\)を平方完成すると\(\{x-(a+2)\}^2+a^2+4a+b+4\)

平方完成についてはコチラ↓

したがって、頂点の座標は点\((a+2,a^2+4a+b+4)\)です。

エ　オ・カ

頂点が直線\(y=-4x-1\)上にあるとのことなので…\(x=a+2\)と\(y=a^2+4a+b+4\)を\(y=-4x-1\)に代入します。

代入した式を変形すると、

\[b=-a^2-8a-13\]

となります。

問題【後編】

解説【後編】

キ・ク・ケ

\(x\)軸と異なる2点で交わるということは、判別式\(D>0\)ですから、

\(D=b^2-4ac=(2a+4)^2-4\cdot(-1)\cdot(-a^2-8a-13)>0\)

整理すると、\(a\)の範囲は

\[a<\frac{-9}{4}\]

です。

コ　サ

\(x\)軸の正の部分と負の部分の両方で交わるためには、\(y\)軸と正の値で交わる必要があります。グラフで描くと↓のような状態です。

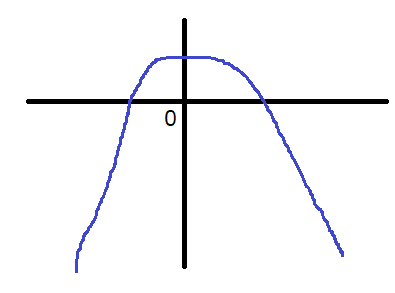
\(G(0)>0\)より、\(-a^2-8a-13>0\)

これを解くと、\(a\)の範囲は…

\[-4-\sqrt{3}<a<-4+\sqrt{3}\]

となります。

シ・ス　セ

\(0\text{≦}x\text{≦}4\)の中で、最小値-22を取る可能性があるのは\(x=0\)と\(x=4\)です。

関数の式は\(y=-x^2+(2a+4)x-a^2-8a-13\)です。\(x=0\)と\(x=4\)をそれぞれ代入します。

すると、

\(-a^2-8a-13=-22\text{・・・①}\)

\(-16+4(2a+4)-a^2-8a-13=-22\text{・・・②}\)

となります。

①から\(a=-9,1\)、②から\(a=-3,3\)

①は\(x=0\)の時に最大値を取る場合です。そのためには頂点の\(x\)座標が2以上の必要がありますので、

\(a+2\text{≧}2\)より\(a\text{≧}0\text{・・・③}\)

①と③より、\(a=1\)

②は\(x=4\)の時に最大値を取る場合です、先程と同様に考えると

\(a+2\text{≦}2\)より\(a\text{≦}0\text{・・・④}\)

②と④より、\(a=-3\)

ソ・タ・チ

\(a=1\)のときの関数の式は、\(y=-x^2+6x-22\)です。頂点は点\((3,-13)\)となり、頂点の\(x\)軸は定義域の範囲内ですから、最大値は-13です。

ツ　テ・ト・ナ

\(a=-3\)の時の関数の式は\(y=-x^2-2x+2\)となり、頂点は点\((-1,3)\)です。

したがって、\(x\)軸方向に4、\(y\)軸方向に-16だけ動かすと、\(a=1\)のときのグラフと一致します。

まとめ

今回の問題を解く上での重要ポイントをまとめてみました。

ということで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。

最後までお読みいただき、ありがとうございました。