【2次関数】センター試験の問題を解いてみた(2018年度)①
今回は、2018年度のセンター試験・本試験で出題された問題を解いていきたいと思います。問題はセンター試験の公式サイトで公開されています。
問題【前編】

解説【前編】
サ・シ
頂点の\(x\)座標は、平方完成をすることで導くことができます。
\(f(x)=ax^2-2(a+3)x-3a+21\)を平方完成します。すると…
\[f(x)=a(x-\frac{a+3}{a})^2-\frac{(a+3)^2}{a}-3a+21\]
となります。
\[\frac{a+3}{a}\]
すなわち
\[1+\frac{3}{a}\]
が頂点の\(x\)座標となります。
ス
2次関数の最小値が\(f(4)\)となるときの\(a\)の値の範囲です。
\(f(4)\)が最小値となるようなグラフをザっと描いてみましょう。
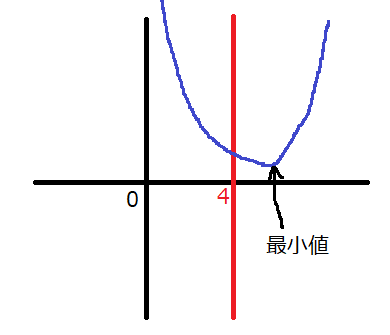
次の2つのどちらかの状態の時に、\(f(4)\)が最小値を取ると言えるでしょう。
(1)頂点の\(x\)座標が定義域の外(0~4より大きな値)である
(2)頂点の\(x\)座標が4である
つまり、頂点の\(x\)座標が4以上であるときに\(f(4)\)で最小値を取ると言えますね(定義域が0~4の時の話です)。頂点の\(x\)座標は先程求めましたね。したがって、次の不等式を解けばいいです。
\[1+\frac{3}{a}\text{≧}4\]
すなわち、\(a\text{≦}1\)です。
ここで気を付けなければいけないことがあります。問題の冒頭で「\(a\)を正の実数とする」という風に記載があるので、\(a>0\)という条件も忘れてはいけません。
したがって、これら2つを満たす\(0<a\text{≦}1\)が正解です。
問題【後編】
解説【後編】
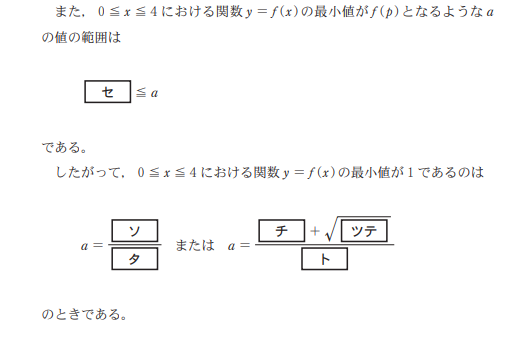
セ
\(f(p)\)というのは頂点のことです。つまり、最小値が頂点であるときの\(a\)の値について問うているわけですね。
頂点が最小値であるためには、定義域(0~4)の中に頂点が含まれていればいいわけですね。
つまり、\(0\text{≦}p\text{≦}4\)となればいいのです。
\(1+\frac{3}{a}\text{≧}0\)かつ\(1+\frac{3}{a}\text{≦}4\)が成立するような\(a\)の範囲は、\(a\text{≧}1\)です。したがって、\(a\text{≧}1\)が答えです。
ソ・タ チ・ツ・テ・ト
最後は、\(0\text{≦}x\text{≦}4\)における\(f(x)\)の最小値が1であるときの\(a\)の値を求めるという問題です。2次関数において、下に凸(\(x^2\)の係数が正)のグラフでは最小値は3パターンあります。
(1)定義域の左端(今回であれば\(x=0\))で最小値を取る場合
(2)頂点がそのまま最小値になる場合
(3)定義域の右端(今回であれば\(x=4\))で最小値を取る場合
ではそれぞれについて見ていきましょう。
(1)についてですが、今回の場合は考えないでよいです。なぜかというと、頂点の\(x\)座標が0より大きいからです。
頂点の\(x\)座標は、\(1+\frac{3}{a}\)でしたね。\(a\)は正の実数なので、\(a\)がどれだけ小さくてもどれだけ大きくても\(1+\frac{3}{a}\)は必ず正の値になります。
したがって、頂点の\(x\)座標が0以下になることはないので、今回は無視して大丈夫です。
では(2)について考えていきましょう。
頂点の\(y\)座標…さきほど平方完成していたので、その結果を利用できますね。
\[f(x)=a(x-\frac{a+3}{a})^2-\frac{(a+3)^2}{a}-3a+21\]
したがって、頂点の\(y\)座標は、
\[-\frac{(a+3)^2}{a}-3a+21\]です。これが1になるということは、
\[-\frac{(a+3)^2}{a}-3a+21 = 1\]
これを解くと、
\[a=\frac{7\pm\sqrt{13}}{2}\]
となります。
ただし、ここで答えになるのは、\(\frac{7+\sqrt{13}}{2}\)のみです。なぜかというと、先程セのときに\(a\text{≧}1\)という条件を出しており、\(\frac{7-\sqrt{13}}{2}\)これを満たさないからです。少し前に説明した(1)~(3)の中の(2)について説明をしているわけですが、定義域の中に頂点がある場合の条件を求める問題がセだったわけですね。セの問題と繋がっているんです。
\[a=\frac{7+\sqrt{13}}{2}\]
順番が前後しますが、チツテトの答えはこれで分かりました。
最後に、(3)について考えていきましょう。
関数の式に\(x=4\)を代入すると…
\[f(4)=16a-2(a+3)\cdot4-3a+21\]
さらに、\(f(4)=1\)であるから、
\[16a-8(a+3)-3a+21=1\]
この式が成立します。これを解くと、
\[a=\frac{4}{5}\]が出てきます。これがソタの答えです。
まとめ
今回も重要ポイントをまとめます。
- 下に凸のグラフでは最小値は以下の3パターンがある。それぞれの場合について最小値を考える必要がある。
- 頂点が定義域の中の場合
- 頂点が定義域よりも左にある場合
- 頂点が定義域よりも右にある場合
- 頂点が定義域の中にある場合のみ頂点を最小値とみなす
こんな感じですね。今回は特に難しい内容は含まれていなかったかと思います。最小値の本質を理解できていれば満点も容易に取れる問題だったかと思います。ただ、時間との戦いですね(笑)。
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。