【2次関数】センター試験の問題を解いてみる①
Contents
問題
今回はセンター試験の問題を使って解説を行いたいと思います。教科書や参考書で知識をインプットするのもいいですが、それを実際に問題の中で使ってアウトプットすることで理解が深まります。使わない知識は忘れていきます。知識をインプットしたら問題演習の中で使ってアウトプットしていきましょう!
では、その問題について見ていきましょう。実際のセンター試験は穴埋め形式なのですが、ブログの編集の都合で少し問題の形式を変えています。実際の問題を知りたい方は、以下のリンクからどうぞ。
令和2年度本試験の問題(数学Ⅰ・数学Aを選択するとpdfファイルの問題を見ることができます)
問題の内容は変わっていません。ただ、実際の問題の穴埋めをこのブログで表記することが難しいので出題形式を変えています。
\(c\)を定数とする。2次関数\(y=x^2\)のグラフを、2点\((c,0), (c+4,0)\)を通るように平行移動して得られるグラフを\(G\)とする。
(1)\(G\)をグラフに持つ2次関数は、\(c\)を用いてどのように表せるか。
(2)2点\((3,0), (3,-3)\)を両端とする線分と\(G\)が共有点を持つような\(c\)の値の範囲を求めよ。
(3)\(c\text{≧}2\)の場合を考える。\(G\)が点\(3,-1)\)を通るとき、\(G\)は2次関数\(y=x^2\)のグラフをどれだけ平行移動したものであるか。また、このときの\(y\)軸と\(G\)の交点の\(y\)座標を求めよ。
(1)はあることに気づけば簡単に解けるんですが、そこに気づけないと溺死してしまうかもしれません…。
(1)が解けないとその先の問題を解くことはできないので、(1)は何としても正解したいところです。
問題文の中の2点\((c,0), (c+4,0)\)を通るという部分に着目しましょう。2次関数のグラフの概形を頭に思い浮かべてみてください。この2点はどちらも\(y\)の値が0なので、\(x\)軸上の座標を表しています。すると頂点の\(x\)座標が分かるから…。
回答
(1)\(G\)をグラフに持つ2次関数は、\(c\)を用いてどのように表せるか。
ポイント:\(G\)は2点\((c,0), (c+4,0)\)を通るから、頂点の\(x\)座標は\(c+2\)
これが(1)を解くカギです。たとえば、\(y=x^2-4\)であれば、\(x\)軸との交点の\(x\)座標は-2と2であり、頂点の\(x\)座標は0です。この問題であれば、\((c,0)\)と\((c+4,0)\)の2つが\(x\)軸との交点なので、頂点の\(x\)座標は\(c+2\)です。これは2次関数の、頂点を境に左右対称であるという性質によるものです。
このカギを使って回答を進めていきます。
平方関数を表した関数式を\(y=a(x-p)^2+q\)とします。この\(G\)は\(y=x^2\)を平行移動したものであるため、\(a\)は1ですね。したがって、\(y=(x-p)^2+q\)となります。
頂点の\(x\)座標が\(c+2\)であることを先程の式に盛り込みます。すると…
\(y=\{x-(c+2)\}^2+q\)
さらに、\((c,0)\)を通るので、\(x=c\)と\(y=0\)を代入します
\(0=\{c-(c+2)\}^2+q\)
これを解くと、\(q=-4\)となります。したがって、関数式は\(y=\{x-(c+2)\}^2-4\)となります。
そして、導いた式を整理します。展開して2次項と1次項と定数項に分けます。
\(y=x^2-2(c+2)x+(c+2)^2-4\)
\(y=x^2-2(c+2)x+c^2+4c\)
定数項を\(c\)で括ると…
\(y=x^2-2(c+2)x+c(c+4)\)になります。これが(1)の答えです。
(2)2点\((3,0), (3,-3)\)を両端とする線分と\(G\)が共有点を持つような\(c\)の値の範囲を求めよ。
2点\((3,0), (3,-3)\)を両端とする線分と\(G\)が共有点を持つ状態とは、どのような状態でしょうか。文章だけ見て分からない時は、サッとグラフを描いてみましょう。自分で分かればどれだけ雑でも構いません。人に採点されるものでもないですからね(笑)。
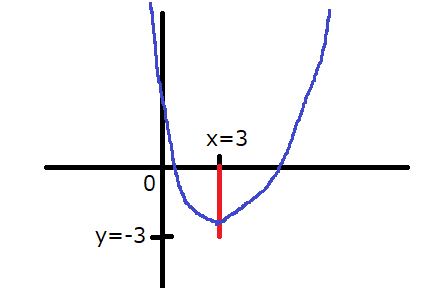
恐らくこんな感じですね。赤線が問題文の中の線分です。青が\(G\)です。\(c\)の値が不定なので正確にグラフを描くのは不可能です。私が図示したものを見ると頂点が線分上にあるように見えますが、別に頂点が線分上にあるとは限りません。グラフのどこかの部分が線分上にあればいいのです。
この線分と\(G\)が共有点を持つための条件はどのようなものでしょうか。それは、以下の2つです。
- \(G\)の\(x\)座標が3のときに\(y\)座標は0以下の値を取る
- \(G\)の\(x\)座標が3のときに\(y\)座標は-3以上の値を取る
この2つの条件を満たすときに、\(G\)と線分が共有点を持つと言えるでしょう。
では、上2つの条件を満たすように不等式を立てて解いていきましょう。
まず、1つ目の条件について式を立てましょう。
(1)より、関数の式が\(y=x^2-2(c+2)x+c(c+4)\)です。
先程の条件により、\(0\text{≧}3^2-2(c+2)\cdot3+c(c+4)\)という式を立てることができます。これを解きます。すると、\(-1\text{≦}c\text{≦}3\)になります。
では、同様に2つ目の条件について式を立てて解いてみましょう。
すると、\(c\text{≦}0,2\text{≦}c\)という答えが出てきます。
赤線の2つを共に満たす範囲が答えです。
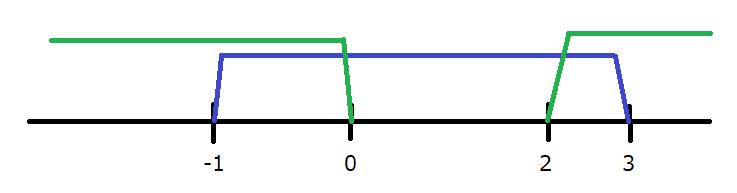
したがって、正解は、\(-1\text{≦}c\text{≦}0,2\text{≦}c\text{≦}3\)となります。
(3)\(c\text{≧}2\)の場合を考える。\(G\)が点\(3,-1)\)を通るとき、\(G\)は2次関数\(y=x^2\)のグラフをどれだけ平行移動したものであるか。また、このときの\(y\)軸と\(G\)の交点の\(y\)座標を求めよ。
では、最後の(3)の問題に行きましょう。といっても(3)は問題が2つあるので、実質あと半分です。
まずは、グラフがどれだけ平行移動しているかを求めましょう。(1)より、グラフの式は、\(y=x^2-2(c+2)x+c(c+4)\)です。点(3,-1)を通るので、\(x=3\)と\(y=-1\)を代入すると…
\(-1=9-6(c+2)+c(c+4)\)
整理すると、\(c^2-2c-2=0\)という式になります。
この式を解くと、\(c=1\pm\sqrt3\)が出てきます。
問題の中で\(c\)の範囲が2以上と指定されているので、\(c=1+\sqrt3\)を適用します。
\(G\)の式に\(c\)の値を代入すると…
\(y=x^2-2\{(1+\sqrt3)+2\}x+(1+\sqrt3)\{(1+\sqrt3)+4\}\)という式になります。
式を整理して平方完成すると…
\(y=\{x-(3+\sqrt3)\}^2-4\)という式になります。したがって、\(y=x^2\)のグラフを\(x\)軸方向に\(3+\sqrt3\)、\(y\)軸方向に\(-4\)平行移動させたものです。
最後に\(y\)軸と\(G\)の交点の\(y\)座標についてです。
\(y\)軸上の座標は\(x\)座標が0です。ですので、先程の\(G\)の式に\(x=0\)を代入します。
つまり、\(y=x^2-2\{(1+\sqrt3)+2\}x+(1+\sqrt3)\{(1+\sqrt3)+4\}\)に\(x=0\)を代入するので、答えは\((1+\sqrt3)\{(1+\sqrt3)+4\}\)です。整理すると、\(8+6\sqrt3\)です。
まとめ
長くなってしまったので、最後に答えだけまとめておきます。
(1)\(y=x^2-2(c+2)x+c(c+4)\)
(2)\(-1\text{≦}c\text{≦}0,2\text{≦}c\text{≦}3\)
(3)\(y=x^2\)のグラフを\(x\)軸方向に\(3+\sqrt3\)、\(y\)軸方向に\(-4\)平行移動させたもの、\(y\)座標は\(8+6\sqrt3\)
今回の問題を解く上で大事なポイントは、
- 2次関数は頂点を境に左右対称のグラフである
- グラフと線分の共有点を持つ=線分の両端の中をグラフが通るような2つの不等式を立てる
という2点かなと思います。あと、個人的には(3)よりも(2)の方が難易度が上な気がしますね。
ということで、今回の内容はここまでです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。