【数学Ⅰ】sin^2θ+cos^2θ=1の証明
今回は、三角比のsin、cos、tanのそれぞれの相互関係を式で表すということをやってみたいと思います。
結論
結論から示しますと、sin、cos、tanの相互関係を示すと、以下のようになります。
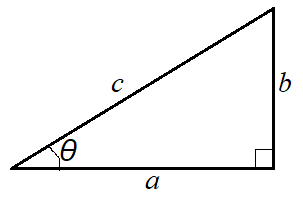
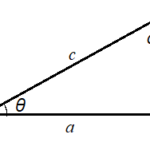
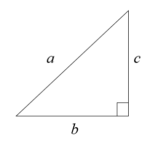
図1の直角三角形において、以下の関係が成り立つ。
(1)\[ \tan \theta = \frac{\sin \theta}{\cos \theta} \]
(2)\[ \sin^2 \theta + \cos^2 \theta = 1 \]
(3)\[ 1 + \tan^2 \theta = \frac {1}{\cos^2 \theta} \]
三角比や三角関数を学習したことがあるなら誰もが見たことのある公式ではないでしょうか?
これらの公式、実はそんなに難しい知識は使うことなく証明することが可能です。
証明のために必要な知識は、過去に紹介していますので、参考にしてみてください。
次の2つのページで紹介した内容をもとに証明していきます。
証明
(1)式について
図の三角形において、
\[ b = c \sin \theta \] \[ a = c \cos \theta \]
です。
ここで、
\[ \tan \theta = \frac{b}{a} \]
であることから、
\[ \tan \theta = \frac{c \sin \theta}{c \cos \theta} = \frac{\sin \theta}{\cos \theta} \]
となります。よって、(1)式の証明が終了です。
(2)式について
三平方の定理より、
\[ c^2 = a^2 + b^2 \]
が成り立つ。
この式に、\[ a = c \cos \theta \]と\[ b = c \sin \theta \]を代入すると、
\[ c^2 = (c \cos \theta)^2 + (c \sin \theta)^2 \]
\[ c^2 = c^2(\cos^2 \theta + \sin^2 \theta) \]
両辺をcの2乗で割ることによって、
\[ \sin^2 \theta + \cos^2 \theta = 1 \]
となります。これで(2)式の証明は終了です。
(3)式について
(2)式の両辺をcosθの2乗で割ります。
すると、
\[ \frac{\sin^2 \theta}{\cos^2 \theta} + 1 = \frac{1}{\cos^2 \theta} \]
となります。これを整理すると、
\[ \tan^2 \theta + 1 = \frac{1}{\cos^2 \theta} \]
となります。これにて、(3)式の証明は終了です。
例題
問.tanθ=3のとき、cosθとsinθを求めよ。
このような問題があったとしましょう。
先程紹介した相互関係を利用することで、計算することができますね。
(3)式より、
\[ 1 + 3^2 = \frac{1}{\cos^2 \theta} \]
\[ \cos^2 \theta = \frac{1}{10}\]
cosθ > 0であるから、
\[\cos \theta = \frac{1}{\sqrt{10}} \] となります。
また、(2)式より、
\[ \sin^2 \theta = 1 – \frac{1}{10} = \frac{9}{10} \]
sinθ > 0であるから、
\[ \sin \theta = \frac{3}{\sqrt{10}} \] となります。
2乗の時の指数の位置について
sinθやcosθ、tanθを2乗するときには、指数の位置に気を付けましょう。
θの前に指数を書くようにします。
まとめ
今回は、sinθとcosθとtanθの関係を表す式と、その証明について紹介しました。
また、それらの式を用いた例題についても扱いました。
先程も記載しましたが、sinθなどを2乗するときは指数を書く位置に気を付けましょう。
今回はここで終わりです。
最後までお読みいただき、ありがとうございました。