【sinθが分かれば超簡単】cosθとtanθについて解説します
今回の内容はcosとtanです!cosとtanで記事を分けようと思っていましたが、sinの考え方が理解できていればcosとtanについては瞬殺できるので、2つ一気に説明します。
では早速、cosとtanがどのように定義されているのかを見ていきましょう。
cosとtanの定義
cosは余弦を導く三角関数である。余弦とは、直角三角形における、角と直角に挟まれる辺の長さの、直角に相対する辺の長さに対する比。
tanは正接を導く三角関数である。正接とは、直角三角形における、角と直角に挟まれる辺の長さの、角に相対する辺の長さに対する比。
三角関数とは何か、という部分についてはsinについての記事で扱っています。参考にしてみてください。
先程の、定義の文章は紐解けたでしょうか。図を使って先程の文章を整理しましょう。
まずはcosについてです。
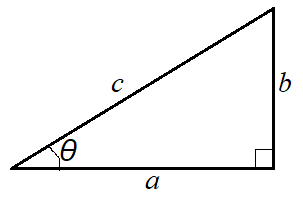
cosθについて
先程の文章によると、cosは余弦を導く関数ですね。その余弦とは「角と直角に挟まれる辺の長さの、直角に相対する辺の長さに対する比。」なので、図1の場合は、
「aの長さのcの長さに対する比。」であることが分かります。「直角に相対する辺の長さ」についてはsinθの記事の中で説明してます。
「角と直角に挟まれる辺の長さ」についてですが、上図で言うと、角というのはθのことです。直角とθに挟まれる辺はaのことを言っています。
整理すると、cosというのは、「aをcで割る」という計算をする関数ですね。
tanθについて
cosと同様にtanについても考えてみましょう。
tanは正接を導く三角関数であり、正接は角と直角に挟まれる辺の長さの、角に相対する辺の長さに対する比。
つまり、正接はbをaで割ることで求められます。この正接を導く関数の名前がtanというわけですね。
まとめ
cosは余弦を導く関数であり、tanは正接を導く関数です。
cosθとtanθは以下のように求められます。

図2のとき、cosθの値は、\[ \cos \theta = \frac{a}{c} \]
tanθの値は、\[ \tan \theta = \frac{b}{a} \]
によって求めることができます。
cosとtanの使い方
「cos」と表記したり「cosθ」と表記したりしますが、「cos」はあくまでも関数名です。
tanについても同様です。実際にcosやtanがどのように使われるのか見てみましょう。
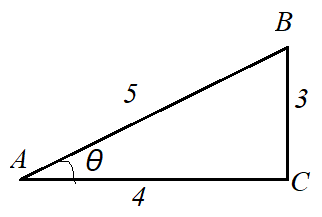
問「図3のcosθとtanθの値を求めよ。」
学校の定期試験では上のような問題が出ると思います。
cosθとtanθの値を求めるという問題ですが、θというのは角度の大きさが不明なので文字で置いてると考えてもらって構いません。
たとえば、cos30°の値を求めよ、の場合は、角度が30°のときにcos関数が出力する値はいくらか。と同じ意味です。
なので、今回の問いは、角度がθのとき、cos関数とtanθはどのような値を出力するか?ということです。
先程のまとめに書いた式を使って求めてみましょう。
cosθの値とtanθの値は、
\[ \cos \theta = \frac{4}{5} \]
\[ \tan \theta = \frac{3}{4} \]
になりますね。
いかがだったでしょうか。これで、sinとcosとtanについての説明が終わりました。sinやcos、tanを使った公式は沢山あるのですが、また別の機会に説明していきたいと思います。
では今回はここで終わりです。最後までお読みいただき、ありがとうございました。
