【力学】いろいろな力②
この記事は、後編です。前編はコチラ↓
重力、張力以外の力を紹介していきます。
垂直抗力
あらゆる物体に重力が働いているわけですが、例えば、本を机に置いた場合、本はそれ以上落ちていきません。
本来は、机を壊して下に落ちていきそうなんですが、重力を阻止している力があります。
それが、垂直抗力です。
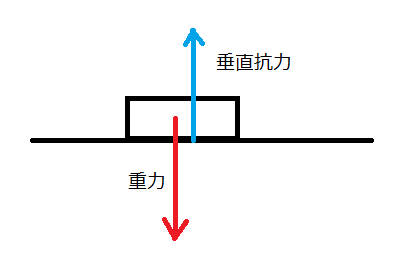
垂直抗力は、接触している物体の面が他の物体に対して、面と垂直な方向に及ぼす力です。
摩擦力
先程の垂直抗力のときのように、本を机の上に置いている状態を考えます。
ここで、水平方向に力を加えると、面は物体に対して運動を妨げるような力を及ぼします。
この力のことを、摩擦力といいます。
摩擦力には静止摩擦力と動摩擦力があります。
静止摩擦力
水平方向に力を加えているのに物体が動き出さない状態であるとき、その物体は面から静止摩擦力を受けています。
要は、静止している物体が受けている摩擦力のことを静止摩擦力といいます。
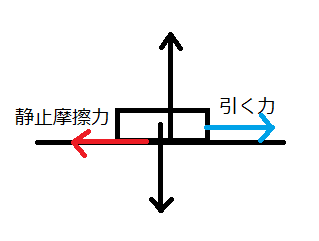
この状態で引く力を大きくしていくと、物体はいつか必ず動き出します。この動き出す直前の静止摩擦力のことを、最大摩擦力といいます。
最大摩擦力の説明は今回は端折ります。
動摩擦力
動いている物体にはたらく摩擦力を、動摩擦力といいます。
動摩擦力の説明も今回は端折ります。
摩擦力が働くのは、荒い地面だけです。
なめらかな地面の場合は、摩擦力の存在を無視することができます。
「あらい」という単語が出てきたら、まず摩擦力の問題を疑ってみるというのもいいかもしれません。
弾性力
ばねにおもりをつけた場合を考えます。
ばねは元の長さに戻ろうとします。このとき、おもりに対してばねは伸びと反対向きの力を及ぼします。
このような、力が加わって変形した物体が元の状態に戻ろうとする力を弾性力といいます。
フックの法則
ばねの弾性力の大きさと、伸びの長さの間には比例関係があります。これをフックの法則と言います。
\[F=kx \text{ ・・・(38)}\]
\(F\)は弾性力を表していて、単位はN(ニュートン)です。
\(k\)は比例定数であり、ばねによって定まるのでばね定数と言います。単位はN/mです。
\(x\)はばねの伸びた長さを表しており、単位はmです。
例題
つる巻きばねを手で引いて\(0.30\)m伸ばしたところ、手はばねから\(6.0\)Nの大きさの力を受けた。
ばね定数は何N/mか。
\(F=kx\)より、
\(6.0=k\cdot 0.30\)
したがって、\(k=20\)N/m
まとめ
- 面が物体に対して面と垂直な方向に及ぼす力を垂直抗力という。
- 面が与える物体の運動を妨げるような力を、摩擦力という。
- 摩擦力には静止摩擦力と動摩擦力の2種類がある。
- 力が変わって変形した物体が、元の状態に戻ろうとする力を弾性力という。
- ばねの弾性力の大きさと伸びの長さが比例することを、フックの法則という。
ということで、今回の記事はここまでです。何か参考になる情報があれば嬉しいです。
他の物理についてのページを見たい方はコチラ↓
最後までお読みいただき、ありがとうございました。