【画像・音声】データの表現について
世の中には様々な種類のデータが存在しています。写真、動画、音声など…。
例えばミュージシャンがライブを開催していて、そのライブの模様をDVD化します!っていうときには、コンピュータが処理を行うわけですよね。
このライブでミュージシャンが奏でた音楽というのは、本来はアナログデータです。アナログとは、連続している情報、とかそういう意味です。
このときに、どの曲のどの部分でどのカメラの映像を使って…とかいう編集の話はさておき、DVD化するためにはコンピュータでライブの模様から映像データを作ります。
この映像データがそれぞれのDVDに記録されてDVDショップに並ぶわけですが…
この映像データというのは、アナログデータではなくディジタルデータです。ディジタルとは、離散的とか、そんな感じの意味合いです。
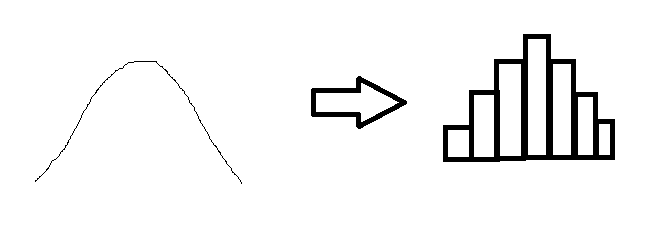
ここまでいろいろ書いてきましたが、要は、左図のような曲線を、右図のような値が飛び飛びのグラフに変換する作業が"アナログデータからディジタルデータへの変換作業"ということです。
このアナログからディジタルへの変換作業については音声データを例に解説します。
Contents
画像データについて
ドット
変換作業の前に、データについての理解を深めましょう。
画像データというのは、点の情報が集まったものです。
私たちが普段使っているスマホやPC、テレビなどの画面をすごく近い距離で見てみてください(目が悪くならない程度に…笑)
すると、電子機器の画面がすごく小さな無数の点(ドット)の集まりであるというのが何となく分かると思います。
このドットの数を解像度と表したりします。ドットが多い状態を解像度が高い…など。
このドットの数が多ければ多いほど、画像を滑らかに表現でき、少なくなればなるほど、画像が荒くなります。いわゆる画質が悪いっていうやつですね。
ドット数が増えれば増えるほど、画像のデータは大きくなります。しかし、画像のデータが大きくなる要因は、ドットの数だけではありません。
色情報
画像というのは、当然、色についての情報が必要です。画面にある無数のどっとのうち、このドットを何色にして、隣のドットは何色にして…という風にして、画像全体としての色が決まります。
この、色についてですが、より多くの色を実現しようと思うと、画像データが増えていきます。白黒画像よりカラー画像の方がほぼ確実に画像のデータ量は大きくなるでしょうね。
白と黒の2色だけであれば、1ドットにつき1ビットの情報量が必要です。1ビットで0と1の2種類を表すことができ、0を白、1を黒と決めておけば2色表現できますよね。
16色であれば4ビット必要で、65536色であれば16ビット必要で…と考えると、色が多くなればなるほど画像データも大きくなるのは、理解していただけるかと思います。
以上の内容をまとめると、
画像データの大きさは、色情報と解像度によって決まる。
例題①
表示解像度が\(1,000\)×\(800\)ドットで、色数が\(65,536\)色の画像を表示するのに最低限必要なビデオメモリ容量は何Mバイトか。
ここで、\(1\)Mバイト=\(1,000\)kバイト、\(1\)kバイト=\(1,000\)バイトとする。
ア \(1.6\)
イ \(3.2\)
ウ \(6.4\)
エ \(12.8\)
表示される総ドット数は、\(1,000\)×\(800\)=\(800,000\)ドット。
色数は\(65,536\)色=\(2^{16}\)色なので、\(16\)ビット必要です。したがって、\(1\)ドットあたりの色情報は\(16\)ビットです。
\(800,000\)ドットすべてで色情報を扱うので…\(16\)×\(800,000\)=\(12,800,000\)ビットが必要です。
\(1\)バイト=\(8\)ビットですから、\(12,800,000\)ビット=\(1,600,000\)バイト
\(1\)kバイト=\(1,000\)バイトですから、\(1,600,000\)バイト=\(1,600\)kバイト
\(1\)Mバイト=\(1,000\)kバイトですから、\(1,600\)kバイト=\(1.6\)Mバイト
したがって、必要なビデオメモリ容量は\(1.6\)Mバイト。アが正解です。
音声データについて
PCM方式
アナログの波形データをディジタル化して数値表現する手法の代表的なものが、PCM(Pulse Code Modulation)方式です。
PCM方式では、音声をすごく短い時間単位で区切っていき、その単位ごとの音程を数値化することで表現します。
連続した波形データを一定時間ごとに区切る標本化、何段階のレベルに分けるかを決める量子化、得たデータを2進数に変換する符号化、という3段階の処理を経ることで、アナログ波形データを2進数に変換します。
詳しく見ていきましょう。
標本化
アナログデータを一定の時間単位で区切って、その時間ごとの信号レベルを標本として抽出する処理を、標本化(サンプリング)といいます。
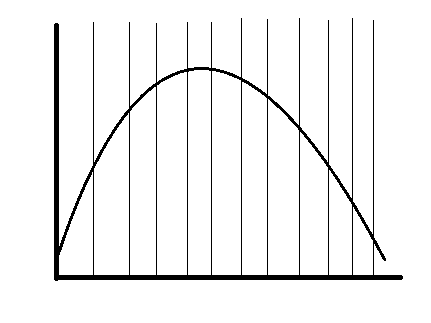
上図のように、細かい間隔に区切ってから、その区切られた間隔のデータの中から1つ標本として取り出していきます。
このとき、区切っていく時間の間隔のことを、サンプリング周期といいます。このサンプリング周期が短ければ短いほど多くのデータ量が必要になります。
単位時間あたりにどれくらい標本が得られるかを示すのが、サンプリング周波数です。サンプリング周波数は、\(\frac{1}{\text{サンプリング周期}}\)という式で得ることができます。
サンプリング周波数はサンプリング周期とは逆で、この値が大きくなればなるほど、データ量は増えていきます。
量子化
標本化は、波形データの横軸に着目して区切っていきました。量子化は、波形データの縦軸着目して区切っていきます。
量子化は、簡単に言うと、原音をどのくらい忠実に再現するかを決める作業です。その再現度合いを表すのが量子化ビット数です。
量子化ビット数が大きければ大きいほど、原音をより忠実に再現できるようになります。
符号化
量子化によって得られた数値を2進数に変換する作業が符号化です。この工程は特に説明不要かと思います。
2進数への変換や、2進数から〇進数への変換については過去に解説していますので、そちらを参考にしてみてください。
ここまでの内容を整理すると…
サンプリング周期が短ければ短いほど、
量子化ビット数が多ければ多いほど、
原音をより忠実に再現できる。
Appleロスレスとは?
最近、音楽サブスクサービスのApple Musicでロスレスというサービスが開始されて話題になっています。
通常、Apple Musicの音質はサンプリング周波数が44.1kHzなんですが、ロスレス音源では最大で192kHzです。ということは、サンプリング周期がすごく短くなるので、より原音に近づくわけですね!
Apple Musicのロスレスについての詳しい情報はコチラ↓
例題②
PCM方式によって音声をサンプリング(標本化)して8ビットのディジタルデータに変換し、圧縮せずにリアルタイムで転送したところ、転送速度は\(64,000\)ビット/秒であった。この時のサンプリング間隔は何μ秒か。
ア \(15.6\)
イ \(46.8\)
ウ \(125\)
エ \(128\)
転送速度は\(64,000\)ビット/秒とあります。この速度で\(8\)ビットのデータを送ると、\(8,000\)回送信できます。
サンプリング回数が\(8,000\)回なので、\(\frac{1}{8000}=0.000125=125\times10^{-6}\)
したがって、サンプリング間隔は\(125\)μ秒となり、答えはウです。
まとめ
- ドット数が増えていくほど、より画像のデータ量は大きくなり、より綺麗な画像を作り出すことができる。
- 1ビットで2色の色情報を持つことができる。
- 音声データをアナログデータからディジタルデータに変換する過程は、標本化・量子化・符号化の3段階である。
- 標本化は、細かい時間で区切ってデータを標本として取り出す。
- 量子化は、サンプリングしたデータを整数値に置き換える。
- 符号化は、置き換えられた整数値を2進数に変換する。
- サンプリング周期が短くなればなるほど、量子化ビット数が大きくなればなるほど、より原音を忠実に再現することができる。
ということで、今回の記事の内容は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。