【三角比】センター試験の問題を解いてみる(2016年度)
2016年度のセンター試験の問題はコチラ↓から閲覧できます。
問題

解答(解説)
ア
問題文の中に\(AB=7\sqrt{3}\)、\(\angle ACB = 60^\circ\)とあります。
これを図に整理したものが下図です。
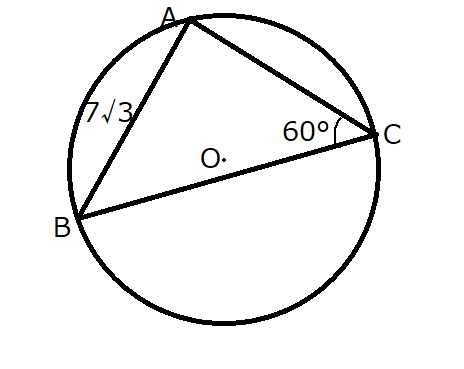
外接円\(O\)の半径は、以下のようにして求めることができます。
\[2R = \frac{AB}{\sin \angle ACB}\]
要するに、ある辺の長さを向かい合う角の\(\sin\)の値で割ればいいわけですね。
今回、\(AB=7\sqrt{3}\)、\(\angle ACB=60^\circ\)と分かっています。\(\sin \angle ACB = \frac{\sqrt{3}}{2}\)ですから、
\(2R = 7\sqrt{3} \cdot \frac{2}{\sqrt{3}}\)
これを整理すると、求める外接円の半径\(R\)は、
\[ R=7\]
イ・ウ・エ
外接円\(O\)の、点\(C\)を含む弧\(AB\)上で点\(P\)を動かす、とあります。
点\(C\)を含む弧\(AB\)というのは、下図の赤線部分のことを指しています。この赤線の上を点\(P\)が動いているというわけです。

ここで、\(\angle PAB\)について考えます。
\(PA\)の長さを\(x\)とすると、\(2PA=3PB\)より、\(PB\)の長さは\(\frac{2}{3}x\)となります。

ここで、余弦定理を使います。
\[AB^2=PA^2+PB^2-2PA\cdot PB \cdot \cos \angle APB\]
余弦定理の公式に各値を代入していきます。
\((7\sqrt{3})^2=x^2+\left(\frac{2}{3}x \right)^2-2\cdot x \cdot \frac{2}{3}x \cdot \cos \angle APB\)
\(x\)を求めるためには、\(\cos \angle APB\)の値が必要ですね。
ここで出てくるのが、円周角の定理です。
円周角の定理については、以下のサイトが参考になるかと思います。
円周角の定理を使うと、\(\angle ACB = \angle APB\)ですから、\(\cos \angle APB = \frac{1}{2}\)となります。
\((7\sqrt{3})^2=x^2+\left(\frac{2}{3}x \right)^2-2\cdot x \cdot \frac{2}{3}x \cdot \cos \angle APB\)に\(\cos \angle APB = \frac{1}{2}\)を代入すると…
\(147 = \frac{13}{9}x^2-\frac{2}{3}x^2\)
これを解くと…
\(x=\pm \sqrt{189}\)
よって、\(PA=\pm \sqrt{189}\)
\(PA>0\)より、
\[PA= \sqrt{189} = 3\sqrt{21}\]
オ・カ
三角形\(\triangle PAB\)の面積は、\(\sin\)関数を使うと、以下のように求めることができます。
\[S=\frac{1}{2} \cdot PA \cdot PB \cdot \sin \angle APB\]
\(\sin \angle APB\)の値は一定なので、変化するのは\(PA\)と\(PB\)だけです。
つまり、\(PA\)と\(PB\)の積が最大の時に、\(\triangle PAB\)の面積は最大になります。
実は、これは知っていればすぐ話を進められるのですが…
一つの円に内接する三角形の中で、面積が最大のものは正三角形であるという法則があります。
\(\angle PAB\)が正三角形の時は\(PA=PB=AB\)ですから、このときの\(PA\)の長さは…
\[PA=7\sqrt{3}\]
キ・ク
\(\sin \angle PBA\)の値が最大となるときはどんなときかと言いますと…\(\angle PBA=90^\circ\)つまり直角の時ですね。
\(\angle PBA=90^\circ\)のときの\(\triangle PAB\)は下図のようになります。

\(PA\)の値を求めていきます。
\(PA \sin \angle APB = AB\)より、
\(PA \cdot \frac{\sqrt{3}}{2} = 7\sqrt{3}\)
これを解くと…
\[PA=14\]
ケ・コ・サ・シ
\(\triangle PAB\)の面積を求めるためには、\(PB\)の長さを求めておく必要があります。
余弦定理より、
\((7\sqrt{3})^2=14^2+PB^2-2\cdot 14 \cdot PB \cdot \frac{1}{2}\)
これを解くと、\(PB=7\)
したがって\(\triangle PAB\)の面積\(S\)は、
\(S=\frac{1}{2}\cdot PA \cdot PB \cdot \sin \angle APB\)より、
\(S= \frac{1}{2} \cdot 14 \cdot 7 \cdot \frac{\sqrt{3}}{2}\)
この式を解くと…
\[S=\frac{49\sqrt{3}}{2}\]
まとめ
2016年度の問題を解くために必要な知識は…
- 余弦定理
- 三角形の面積の求め方
- 外接円の半径の求め方
- 円に内接する三角形の面積
といった感じですね。
というわけで、今回の内容は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。