【鉛直投射】鉛直投げ下ろしと鉛直投げ上げとは?
先日、自由落下について取り扱いました。その記事はコチラ↓です。
今回扱うのは、鉛直投げ下ろしと鉛直投げ上げです。これらの運動と自由落下の違いは、初速があるかどうかです。
自由落下は、重力にすべてを任せているのに対し、鉛直投げ下ろしと鉛直投げ上げは自分で初速を与えてから始まります。
では、具体的に見ていきましょう。
鉛直投げ下ろし
鉛直投げ下ろしとは
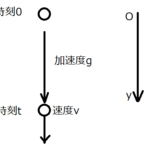
鉛直投げ下ろしというのは、ある高さの点から鉛直下方に向けて、小球を少し勢いをつけて投げ下ろすという運動です。
つまり、鉛直投げ下ろしは、自由落下に初速を加えただけですね。
鉛直投げ下ろし運動の公式
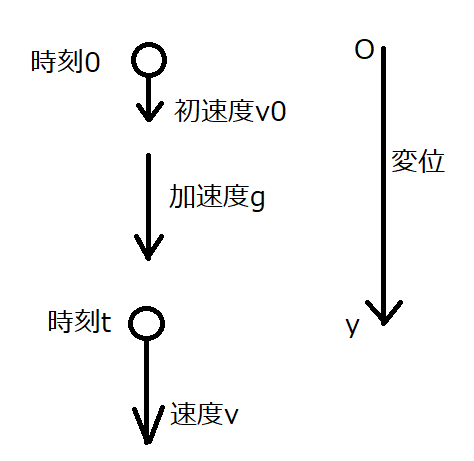
自由落下の公式は、先程リンクを貼った記事にも掲載していますが、以下の3つです。
- \(v=gt\)
- \(y=\frac{1}{2}gt^2\)
- \(v^2=2gy\)
上から①式、②式、③式と呼ぶことにします。
初速度\(v_0\)が加わりますから、①式は、次のようになります。
\(v=v_0+gt\)
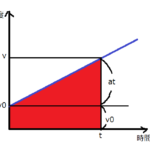
続いて、②式と③式については、自由落下の公式から考えるよりも、加速度の公式を使う方が楽です。
加速度の公式についても、過去の記事で紹介しています。
その中で、
- \(x=v_0 t+\frac{1}{2}at^2\)
- \(v^2-v_0^2=2ax\)
という公式があります。これを④式と⑤式として、使います。
④式を\(x=y\)、\(a=g\)とすると、次の2つの式になります。
- \(y=v_0 t+\frac{1}{2}gt^2\)
- \(v^2-v_0^2=2gy\)
ということで、鉛直投げ下ろしの3つの公式の導出が終わりました。
\[v=v_0+gt \text{ ・・・(19)}\]
\[y=v_0 t+\frac{1}{2}gt^2 \text{ ・・・(20)}\]
\[v^2-v_0^2=2gy \text{・・・(21)}\]
例題
ビルの屋上から、小球を初速度\(2.0\)m/sで鉛直下向きに投げ下ろしたところ、\(4.0\)秒後に地面に達した。重力加速度の大きさを\(9.8\)m/s2として、以下の問いに答えよ。
(1)小球を離した地点の高さを求めよ。
(2)地面に達する直前の小球の速さを求めよ。
(1)\(y=v_0 t+\frac{1}{2}gt^2\)より、
\(y=2.0\cdot 4.0+\frac{1}{2}\cdot 9.8 \cdot 4.0^2\)
これを解くと、求める高さは\(86.4\)m
(2)\(v=v_0+gt\)より、
\(v=2.0+9.8\cdot 4.0\)
これを解くと、求める速さは\(41.2\)m/s
鉛直投げ上げ
鉛直投げ上げとは
先程、鉛直投げ下ろしについて解説しました。
続いては、鉛直投げ上げです。鉛直投げ下ろしが初速を与えて鉛直下方に投げ下ろす運動だったのに対し、鉛直投げ上げは、初速を与えて鉛直上方へ投げ上げる運動です。
最初は上向きの運動になり、ある時点で速度が0になり、最終的に下向きの運動になります。
鉛直投げ上げ運動の公式
投げ上げた点を原点とし、初速度\(v_0\)[m/s]の向きを正の向きとします。\(t\)[s]後の座標を\(y\)[m]、速度を\(v\)[m/s]とします。
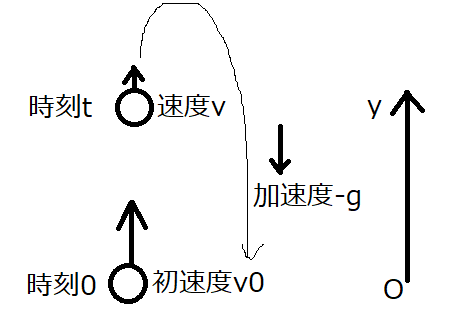
先程の鉛直投げ下ろしの公式の3つを使って、鉛直投げ上げの公式を考えていきます。
\[v=v_0+gt \text{ ・・・(19)}\]
\[y=v_0 t+\frac{1}{2}gt^2 \text{ ・・・(20)}\]
\[v^2-v_0^2=2gy \text{・・・(21)}\]
鉛直投げ下ろしから変化している部分は、加速度の向きが逆になっていることですね。
厳密には加速度の向きは変わっていないのですが、運動の向きが投げ下ろしでは下向きを正としていたのに対し、投げ上げでは上向きを正としているので、加速度の向きを逆として考えます。
したがって、加速度\(g\)が\(-g\)になります。
すると、以下の3つの式が得られます。
- \(v=v_0 – gt\)
- \(y=v_0 t – \frac{1}{2}gt^2\)
- \(v_2-v_0^2=-2gy\)
自由落下と鉛直投げ下ろしは下向きが正、鉛直投げ上げは上向きが正と覚えておきましょう。
\[v=v_0 – gt \text{ ・・・(22)}\]
\[y=v_0 t – \frac{1}{2}gt^2 \text{ ・・・(23)}\]
\[v_2-v_0^2=-2gy \text{ ・・・(24)}\]
例題
小球を初速度\(19.6\)m/sで真上に向けて投げるとき、次の値を求めよ。ただし、鉛直上向きを正とし、重力加速度の大きさを\(9.8\)m/s2とする。
(1)最高点に達するまでの時間\(t_1\)[s]とその高さ\(h_1\)[m]
(2)元の位置に戻るまでの時間\(t_2\)[s]とその時の速度\(v_2\)[m/s]
(1)最高点に達しているとき、速度は\(0\)m/sです。したがって\(v=v_0-gt\)より、
\(0=19.6-9.8t_1\)
これを解くと、\(t_1=2.0\)[s]
その時の高さは、\(y=v_0 t-\frac{1}{2}gt^2\)より、
\(h_1=19.6 \cdot 2.0 – \frac{1}{2} \cdot 9.8 \cdot 2.0^2\)
これを解くと、\(h_1=19.6\)[m]
(2)元の位置というのは変位\(y=0\)の状態です。したがって\(y=v_0 t -\frac{1}{2}gt^2\)より、
\(0=19.6\cdot t_2 – \frac{1}{2} \cdot 9.8 \cdot (t_2)^2\)
これを解くと、\(t_2=0,4\)
\(t_2\text{≠}0\)より、\(t_2=4.0\)[s]
\(v=v_0-gt\)より、
\(v_2=19.6-9.8 \cdot 4.0\)
これを解くと、\(v_2=-19.6\)m/s
まとめ
今回の記事では、鉛直投げ下ろしと鉛直投げ上げについて扱いました。
- 鉛直投げ下ろし運動
- 初速を与えて鉛直下方に投げ下ろす運動である。
- 鉛直下向きが運動の正の方向である。
- 鉛直投げ上げ運動
- 初速を与えて鉛直下方に投げ上げる運動である。
- 鉛直上向きが運動の正の方向である。
- 物体が最高点に達しているとき、速度は0である。
- 物体が元の位置に戻ってきたとき、変位は0である。
ということで、今回の記事はここまでです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。