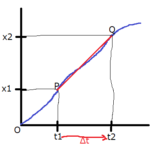
【落体の運動】自由落下
今まで速度や加速度について解説してきました。以下にリンクをまとめていますので、参考にしてみてください。
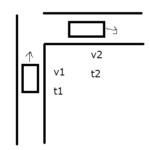
今回から扱う「落体」というのは、これまでの横方向に動く物体の話と違って、縦に動く物体です。
自由落下
自由落下の考え方
自由落下というのは、意図的に力を加えることなく、重力だけを受けて初速度0で鉛直に落下する運動です。
球体をある高さから下に落とします。その状況で加速度を求めると、加速度の大きさが一定になります。鉛直下向きで9.8m/s2という値です。
この加速度の値は、球の質量を変えて実験しても常に同じ値になることが分かっています。
この、落体の一定の加速度のことを、重力加速度といいます。
以上の内容を整理すると、自由落下とは…
初速度の大きさ0、加速度が鉛直下向きに大きさ9.8m/s2の等加速度直線運動である
重力加速度は、\(g\)と表されることが多いです。(重力加速度の英語がgravitational accelerationなのでその頭文字が\(g\))
自由落下の公式
自由落下を始める点を原点として、鉛直下向きに\(y\)軸を取ります。また、\(t\)[s]後の球の座標を\(y\)[m]、速度を\(v\)[m/s]とします。
つまり、下図のような状態です。
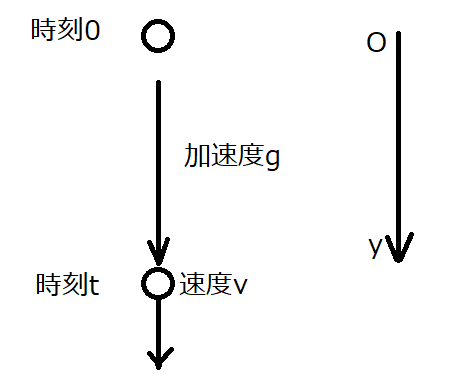
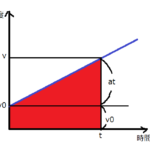
ここで、加速度の公式を使います。3つの公式がありました。この3つの公式については、過去の記事で解説しています。
- \(v=v_0+at\)
- \(x=v_0t+\frac{1}{2}at^2\)
- \(v^2−v_0^2=2ax\)
この式に、値を代入していきます。
自由落下では、初速度は0です。また、加速度は重力加速度であり、常に一定です(\(g=9.8\)m/s2)。変位は\(x\)ではなく\(y\)です。
したがって、\(v_0=0\)、\(a=g\)、\(x=y\)を代入すると、次のような公式が得られます。
\[v=gt\text{ ・・・(16)}\]
\[y=\frac{1}{2}gt^2\text{ ・・・(17)}\]
\[v^2=2gy\text{ ・・・(18)}\]
例題
2階の窓から小球を静かに離すと、2.0秒後に地面に達した。このとき、以下の問いに答えよ。ただし、重力加速度の大きさは9.8m/s2とする。
(1)小球を離した点の高さを求めよ。
(2)地面に達する直前の小球の高さを求めよ。
(1)\(y=\frac{1}{2}gt^2\)に\(g=9.8\)、\(t=2.0\)を代入すると、
\(y=\frac{1}{2} \cdot 9.8 \cdot (2.0)^2\)
これを解くと、小球を離した点の高さは\(19.6\)[m]
(2)\(v=gt\)に\(g=9.8\)と\(t=2.0\)を代入すると、
求める小球の速さは\(19.6\)[m/s]
2階の高さなのに19.6mって恐ろしい高さですね…笑
重力加速度は場所によって違う?
高校物理の中では重力加速度は9.8m/s2とされています。しかし、実際には、計測する場所によって、重力加速度の大きさには少し差があるようです。
例えば、シンガポールでは9.7807m/s2だそうです。ノルウェーの首都オスロでは9.8191m/s2とのこと。
日本国内でも場所によって少し差があるようで、北海道の稚内だと9.8062、東京の羽田だと9.7976、沖縄の宮古島では9.7900だそうです。
こうやって見てみると、確かに場所によって差がありますが、9.8から大きくかけ離れた場所があるわけではなさそうです。ですから、問題を解く時には自信をもって重力加速度は9.8としておいて良さそうですね。
ただし、問題文の中で「重力加速度は9.7とする。」といった文言がある場合は、9.7で計算しなければならないので要注意です。そんな問題は見たことありませんけど(笑)。
まとめ
今回の記事では、自由落下について解説しました。
- 初速度0で垂直に落下する運動を自由落下と言います。
- 自由落下に限らず、鉛直方向の運動の加速度は重力加速度と言い、9.8m/s2で常に一定です。
- 自由落下における公式は以下の3つです。
- \(v=gt\)
- \(y=\frac{1}{2}gt^2\)
- \(v^2=2gy\)
- 重力加速度は場所によって異なることもあるが、9.8m/s2から大きく離れることはない。
ということで、今回の記事はここまでです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。