【三角比】センター試験の問題を解いてみる(2018年度追試)
2018年度追試の問題はセンター試験公式サイトで閲覧可能です↓
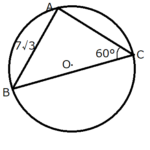
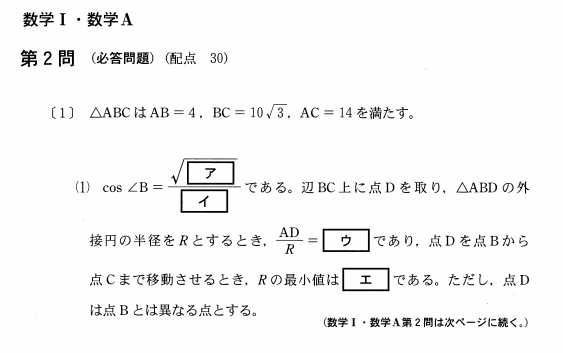
問題【前編】
解答(解説)【前編】
ア・イ
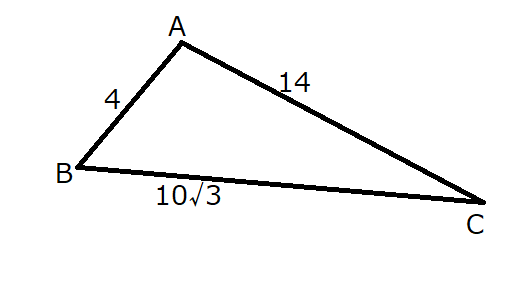
\(\cos \angle B\)を求める問題です。
余弦定理より、
\(\cos \angle B = \frac{4^2+(10\sqrt{3})^2-14^2}{2\cdot 4\cdot 10\sqrt{3}}\)
これを解くと、
\[\cos \angle B = \frac{\sqrt{3}}{2}\]
ウ
\(\cos \angle B = \frac{\sqrt{3}}{2}\)ですから、\(\sin^2 \theta + \cos^2 \theta = 1\)より、
\(\sin \angle B = \frac{1}{2}\)
ここで正弦定理を使います。
\(2R=\frac{AD}{\sin \angle B}\)より、\(\frac{AD}{R}=2\sin \angle B\)という式が出てきます。
\(\sin \angle B\)は先程求めましたので、式に代入すると…
\[\frac{AD}{R}=1\]
エ
先程の式を変形すると、\(R=\frac{AD}{2\sin \angle B}\)となります。
\(\sin \angle B\)の値が変わることはないので、\(R\)が最小になる=\(AD\)の長さが最小になる という関係が成立します。
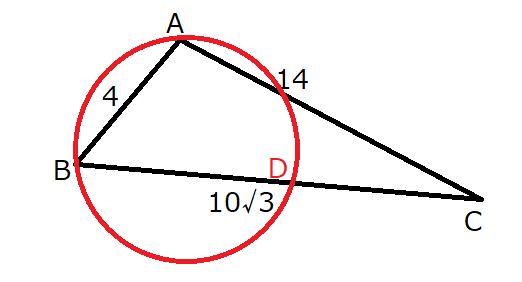
\(AD\)の長さが最小になるときというのはどういうときかと言いますと…
\(BD\)と\(AD\)が垂直、つまり、\(\triangle ABD\)が直角三角形になるときです。
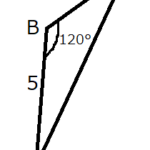
つまり、下図のような状態です。
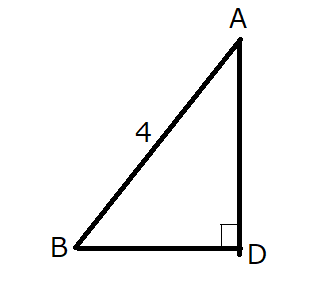
\(\sin \angle B\)の値はすでに求めていますから、
\(AD=AB \sin \angle B = 4\cdot \frac{1}{2}\)
したがって、\(AD=2\)
\(R=\frac{AD}{2\sin \angle B}\)に\(AD=2\)と\(\sin \angle B = \frac{1}{2}\)を代入すると…
\[R=2\]
問題【後編】
解答(解説)【後編】
オ・カ・キ
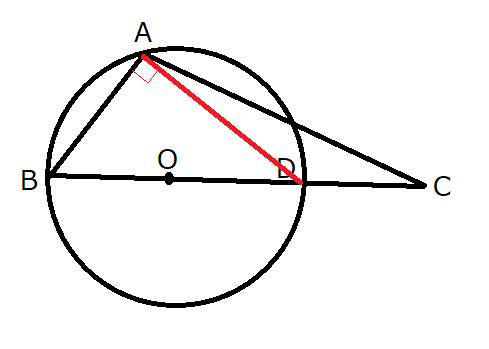
\(BD\)が円の直径ですから、円周角の定理より、\(\angle BAD = 90^\circ\)です。
ということは、\(BD \cos \angle B = AB\)が成り立ちます。
\(AB=4\)、\(\cos \angle B = \frac{\sqrt{3}}{2}\)を代入すると、\(BD=\frac{8\sqrt{3}}{3}\)
\(BD\)が円の直径ですから、半径はその半分です。したがって、
\[R = \frac{4\sqrt{3}}{3}\]
ク・ケ・コ・サ
\(\triangle ABC\)の面積 = \(\triangle ABD\)の面積 + \(\triangle ACD\)の面積ですね。
\(\triangle ABC\)の面積は、\(\frac{1}{2}\cdot AB \cdot BC \cdot \frac{1}{2}\)より、\(10\sqrt{3}\)です。
\(\triangle ABD\)の面積は、\(\triangle ABC\)と同様に求めると、\(\frac{8\sqrt{3}}{3}\)となります。
\(\triangle ACD\)の面積は、\(\triangle ABC\)の面積から、\(\triangle ABD\)の面積を引けばよいので、
求める面積を\(S\)とすると、
\[S = \frac{22\sqrt{3}}{3}\]
まとめ
今回の問題を解く上で必要な知識は…
- 正弦定理
- 余弦定理
- \(\sin\)関数を使った三角形の面積の求め方
- 円周角の定理
といったところでしょうか。
円周角の定理は中学数学の範囲でしたよね…中学生の記憶なんて10年近く前なので、記憶が曖昧ですが…(笑)
ということで、今回の記事の内容は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。