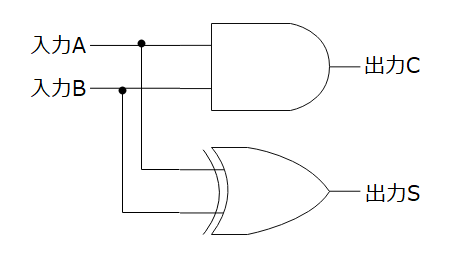
【論理演算】ビット操作
論理演算(ORやANDなど)を使って、ビット操作というものを行うことができます。論理演算(ORやANDなど)については過去の記事で取り扱っていますので、参考にしてみてください↓
今回は、そのビット操作の中で、「ビット反転」「特定ビット抜き出し」という2つの操作について紹介したいと思います。
Contents
ビットの反転
ビットの反転には排他的論理和(EOR、XOR)を使います。
0が入っている桁を1に変更して、1が入っている桁を0に変更する、といった操作ですね。
では、実際の手順を見ていきます。
①反転用ビット列の準備
反転させたい元のビット列に対して、ビットを反転させたい位置に1を入れたビット列を準備します。
今回は、「01010111」というビット列を反転させるとしましょう。8ビットすべて反転させるものとします。
8ビットすべて反転させるので、「1111111」を用意するわけです。
②排他的論理和によって反転
元のビット列と用意したビット列で排他的論理和(EOR、XOR)をとると、元のビット列を反転させた結果を得ることができます。
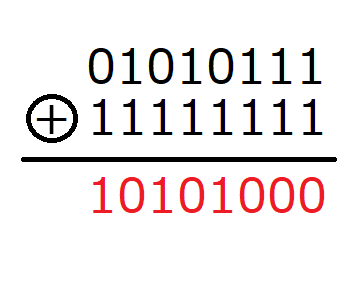
排他的論理和は、2つの入力値が同一であれば0、異なる値であれば1を出力するという特性があります。その特性を利用することで、ビット反転が可能になります。
今回の例とは逆に、「00000000」というすべて0のビット列を用意して排他的論理和をとると、全ビット反転せずにそのまま出力されますね(笑)
ちなみに、「ビットを反転させたい位置に1を入れたビット列」のことをマスクパターンといいます。
このビット操作の知識をしっかり理解しておくと、基本情報技術者試験の「ネットワーク」の項目の中で出てくる、「サブネットマスク」の内容が理解しやすくなると思います。
この「サブネットマスク」については、また別の記事で扱うつもりです。
特定のビットを取り出す
先程の例で使った「01010111」をまた使います。今度は、下位4ビットの情報を取り出す場合を考えます。
ビット取り出しには、「論理積(AND)」を使います。入力値がどちらも1の場合のみ1を出力する、っていうやつです。
では、実際の手順です。
①マスクパターンの準備
今回、取り出し対象のビット列は「01010111」です。ビットを取り出したい位置に1を入れたビット列を、マスクパターンとして準備します。
下位4ビットの情報を取り出すので、「00001111」ですね。
②論理積をとって特定位置のビット取り出し
取り出し対象の「01010111」と、マスクパターンの「00001111」で論理積を取ると、元のビット列から指定した位置のビットだけが取り出せます。

取り出し非対称のビット列は「0」で埋められ、取り出し対象のビット列のみちゃんと取り出すことができました。
例題
負数を2の補数で表すとき、8桁の2進数nに対し、-nを求める式はどれか。
ただし、+は加算を表し、OR、XORはそれぞれビットごとの論理和、排他的論理和を表す。
ア (n OR 10000000) + 00000001
イ (n OR 11111110) + 11111111
ウ (n XOR 10000000) + 11111111
エ (n XOR 11111111) + 00000001
2の補数は、ビット反転させてから1を足すことによって求めます。ビット反転は排他的論理和を使います。そして1を足します。この2つの操作を行っているのはエです。したがって、解答はエです。
まとめ
- ビット反転操作を行う場合は、反転を行わない桁に0、反転を行う桁に1を入れたマスクパターンを用意して、排他的論理和をとる。
- 特定のビットを取り出す場合は、取り出さない桁に0、取り出したい桁に1を入れたマスクパターンを用意して、論理積をとる。
今回の記事の内容は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。