【論理回路】加算器とは何か?
加算器とは
加算器とは何なのでしょうか。それは、文字通り、加算を行う回路のことです。
具体的には、2進数の足し算を行う回路のことを、加算器といいます。
OR回路や、AND回路、EOR回路などを組み合わせて作られています。OR回路やAND回路などは、過去の記事で解説していますので、参考にしてみてください。
加算器には、半加算器と全加算器という2種類があります。それぞれの特徴を見ていきます。
半加算器と全加算器の違い
半加算器は、下位からの桁上がりを考慮しない加算器です。これだけの説明じゃ、よく分かりませんよね。

1桁目の計算は、下位からの桁上がりを考慮する必要がありませんよね。ですから、1桁の計算の場合は半加算器でOKなのです。
一方、2桁目の計算は、1桁目からの桁上がりと2桁目で生じうる桁上がりを両方考える必要があります。
もちろん、桁上がりが生じない可能性もありますけどね。
半加算器の仕組み
1桁同士の足し算は、0 + 0 = 0、0 + 1 = 1、1 + 0 = 1、1 + 1 = 10 の4パターンがあります。
では、足される数を入力A、足す数を入力B、2桁目の数を出力C、1桁目の数を出力Sとして、真理値表にまとめてみましょう。
ではまず、出力Cについて。
| 入力A | 入力B | 出力C |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2桁目の数は、1 + 1 の計算を行ったときにはじめて1になります。
この真理値表を見て、何か気づきませんか?
そうです。論理積(AND)の真理値表と同じですよね。
では、出力Sについてはどうでしょうか。
| 入力A | 入力B | 出力S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
出力Sの真理値表は、排他的論理和(EOR、XOR)の真理値表と同じになりますね。
ここまで来たら、あとは2つの回路を合体させれば半加算器が完成します。つまり、半加算器は↓のような回路です。
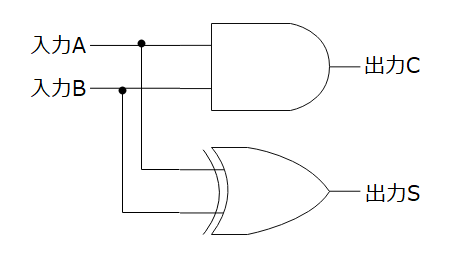
このように、半加算器は、AND回路とEOR,XOR回路を組み合わせることによって、作ることができます。
全加算器の仕組み
全加算器は、下位桁からの桁上がりを考慮するので、入力が1つ増えます。
つまり、↓のような構図になりますね。

では、このような構図を回路で実現させてみましょう。
まず、入力Aと入力Bの加算についてです。これは、半加算器によって実現できます。
続いて、「AとBの加算結果に、下位からの桁上がりを表す入力C’を加算する」という計算は、どうすればいいでしょうか。

AとBの加算結果はSですから、S+C’という計算をやるわけですね。これに必要な回路は…半加算器です。
最後に、出力Cについて考えます。真理値表を書いてみます。
| 入力A | 入力B | 入力C’ | 出力C |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
真理値表を見れば分かりますが、1が2回以上入力されれば出力Cは1になります。これが何を意味するかと言いますと…1桁目か2桁目のどちらか一方で桁上がりが生じるようであれば、出力Cは1になるということです。
以上をまとめると、全加算器は、半加算器2つとOR回路を合体することで実現できます。

例題
図に示す1桁の2進数\(x\)と\(y\)を加算して、\(z\)(和の1桁目)及び\(c\)(桁上げ)を出力する半加算器において、\(A\)と\(B\)の素子の組み合わせとして、適切なものはどれか。

ア A:排他的論理和 B:論理積
イ A:否定論理積 B:否定論理和
ウ A:否定論理和 B:排他的論理和
エ A:論理積 B:論理和
和の1桁目は、\(x\)と\(y\)がともに0もしくは1のときは0となり、それぞれが異なる値の時は1となります。つまり、排他的論理和です。
桁上がりは、\(x\)と\(y\)の両方が1の時のみ1になります。つまり、論理積です。
したがって、解答はアです。
まとめ
- 2進数の加算を行う回路を加算器という。
- 下位からの桁上がりを考慮しない半加算器と、考慮する全加算器がある。
- 半加算器は、論理積回路と排他的論理和回路の組み合わせによって構成されている。
- 全加算器は、半加算器2つと論理和回路の組み合わせによって構成されている。
今回の記事の内容は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。