【三角比】センター試験の問題を解いてみる(2020年度追試)
2020年度の追試験の問題は↓のサイトで閲覧可能です。
問題【前編】

解答(解説)
ア・イ
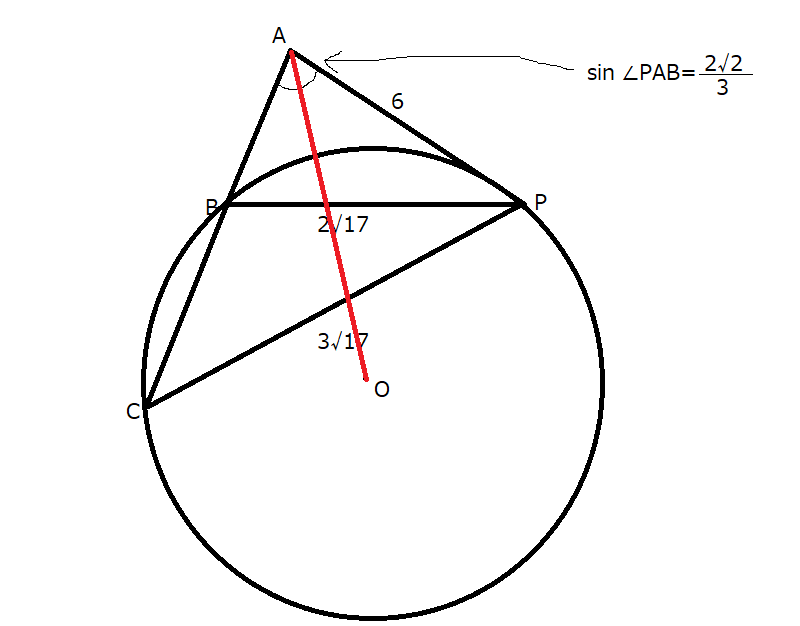
問題の条件を踏まえて雑に図を描いてみます。
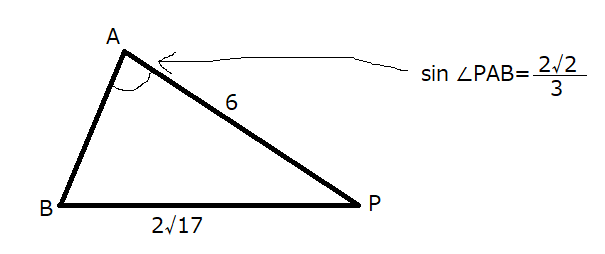
\(\sin^2 \theta + \cos^2 \theta = 1\)より、
\(cos^2 \angle PAB=\frac{1}{9}\)
したがって、\(\cos \angle PAB=\frac{1}{3},-\frac{1}{3}\)
(1)\(\cos \angle PAB=\frac{1}{3}\)のとき
余弦定理より、\((2\sqrt{17})^2=AB^2+6^2-12AB\cdot \frac{1}{3}\)
これを解くと、\(AB=8\)
しかし、問題文に示されている条件である\(AB<AP\)とならないので不正解です。
(2)\(\cos \angle PAB=-\frac{1}{3}\)のとき
(1)と同様に式を立てて解くと、\(AB=4\)となります。こちらは\(AB<AP\)を満たすので、こちらが正解です。したがって、
\[AB=4\]
\(\cos \angle PAB<0\)より、\(\angle PAB\)は鈍角です。
問題【後編】
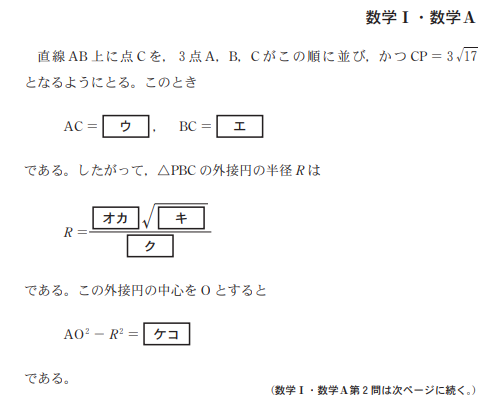
解答(解説)
ウ
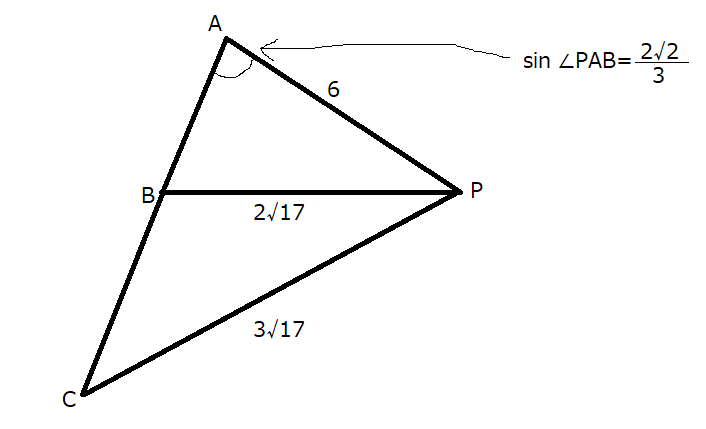
余弦定理より、
\((3\sqrt{17})^2=AC^2+6^2-2\cdot 6 \cdot AC \cdot \left(-\frac{1}{3} \right)\)
これを解くと、
\[AC=9\]
エ
\(BC+AB=AC\)より、
\[BC=5\]
オ・カ・キ
まず、\(\sin \angle BPC\)を求めることにします。
\(\cos \angle BPC\)は、余弦定理により、\(\frac{49}{51}\)
\(\sin^2 \theta + \cos^2 \theta = 1\)より、\(\sin \angle BPC = \frac{10\sqrt{2}}{51}\)
続いて、正弦定理より、
\[2R=\frac{BC}{\angle BPC}\]
各値を代入して解くと、\[R=\frac{51\sqrt{2}}{8}\]
ケ・コ
\(\angle OAB\)と\(\angle OAC\)の大きさが等しくなることに着目します。したがって、\(\sin\)や\(\cos\)の値も等しくなります。これに着目して、余弦定理を使って式を立てます。
\(\cos \angle OAB=\frac{AB^2+AO^2-BO^2}{2AB \cdot AO}\)
\(\cos \angle OAC=\frac{AC^2+AO^2-CO^2}{2AC \cdot AO}\)
この2つの式に各値を入れて=で結びます。ちなみに\(BO\)と\(CO\)は外接円の半径ですから\(R\)と置くことができます。
\(\frac{16+AO^2-R^2}{8AO}=\frac{81+AO^2-R^2}{18AO}\)
72をかけて分母を消したり、いろいろやって整理していくと最終的に答えが出てきます。
\[AO^2-R^2=36\]
最後に
今回の問題は、本試験と同様に、正弦定理と余弦定理を理解していればそこまで難しくはないですね。失点のポイントとしては、計算が少しややこしいことくらいでしょうか。
あとは、\(\cos\)の符号や鋭角・鈍角の知識も必須の内容ですね。この辺の話も教科書で紹介されている内容なので、やはり基本が大事ですね。
というわけで、今回の記事はここまでです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。