【三角比】センター試験の問題を解いてみる(2020年度)
2020年度の数学Ⅰ・Aの問題はコチラで閲覧可能です↓
問題
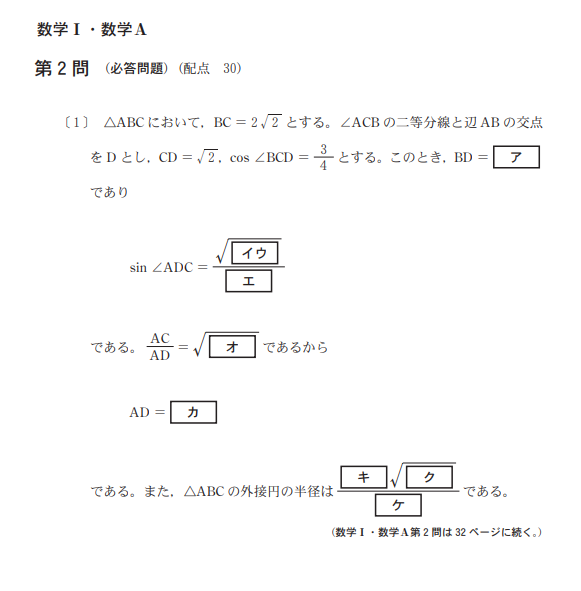
解答(解説)
ア
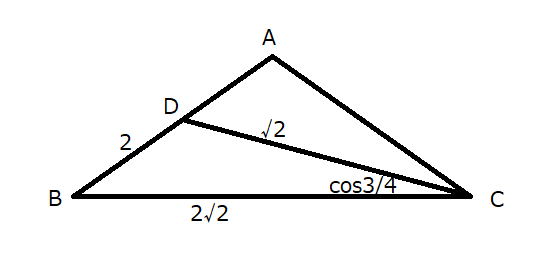
まず、問題の条件を整理して、雑に図を描いてみます。
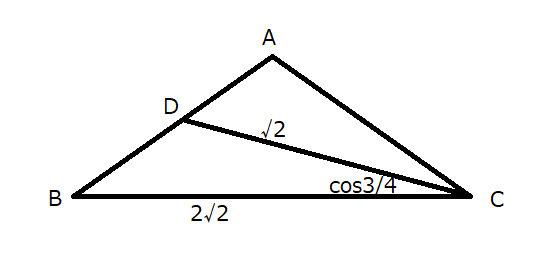
\(BD\)の長さを求めるには、余弦定理を使います。
余弦定理より、\(BD^2=CD^2+BC^2-2CD \cdot BC \cdot \cos\angle BCD\)が成り立ちます。これに値を代入していくと、
\(BD^2=2+8-8 \cdot \frac{3}{4}\)
\(BD^2=4\)
\(BD>0\)より、
\[BD=2\]
イ・ウ・エ
\(\sin \angle ADC\)を求めるためには、2ステップを踏みます。
ステップ1:\(\cos \angle BDC\)を求める
余弦定理を使うと、\(\cos \angle BDC = \frac{2^2+(\sqrt{2})^2-(2\sqrt{2})^2}{2\cdot 2 \cdot \sqrt{2}}\)
したがって、\(\cos \angle BDC = -\frac{\sqrt{2}}{4}\)
ステップ2:\(\cos \angle ADC\)を求める
\(\angle BDC + \angle ADC = 180^{\circ}\)ですから、
\(\cos (180^{\circ}-\theta)=-\cos \theta\)より、
\(\cos \angle ADC=\frac{\sqrt{2}}{4}\)
ステップ3:\(\sin \angle ADC\)を求める
\(\sin^2\theta + \cos^2\theta = 1\)より、\[\sin\angle ADC=\frac{\sqrt{14}}{4}\]
オ
正弦定理より、
\(\frac{AC}{\sin \angle ADC} = \frac{AD}{\sin \angle ACD} \)
\(\frac{AC}{AD}=\frac{\sin \angle ADC}{\sin \angle ACD} \text{・・・①}\)
\(\sin \angle ACD\)についてですが、\(\sin \angle BCD\)と同じです(問題文の\(\angle ACB\)の二等分線…という部分に注目)
\(\cos \angle ACD=\frac{3}{4}\)ですから、\(\sin^2 \theta + \cos^2 \theta = 1\)より、
\(\sin \angle ACD = \frac{\sqrt{7}}{4}\)
①式より、\(\frac{AC}{AD}=\frac{\frac{\sqrt{14}}{4}}{\frac{\sqrt{7}}{4}}\)
したがって、
\[\frac{AC}{AD}=\sqrt{2}\]
カ

\(AC=\sqrt{2}AD\)ですから、余弦定理より、次の式が立ちます。
\((\sqrt{2}AD)^2=AD^2+2-2 \cdot \sqrt{2} \cdot AD \cdot \frac{\sqrt{2}}{4}\)
これを解くと、
\[AD=1\]
キ・ク・ケ
外接円の半径を\(R\)とすると、正弦定理より、\(2R=\frac{AB}{\sin \angle ACB}\)が成り立ちます。
\(\sin \angle ACB\)はまだ不明です。しかし、\(\cos \angle ACB\)は、余弦定理を使えば出せますね。
\(\cos \angle ACB=\frac{1}{8}\)です。
したがって、\(\sin \angle ACB = \frac{3\sqrt{7}}{8}\)ですから、
\(2R=\frac{AB}{\sin \angle ACB}\)より、
\[R=\frac{4\sqrt{7}}{7}\]
最後に
今回の問題は、正弦定理と余弦定理を使い回して解答していくだけでしたね。
正弦定理と余弦定理の解説は、また別の記事で取り上げようと思います。
というわけで、今回の記事は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。